Physik Oberstufe/ Quantenphysik/ Kernphysik

Aufbau und Eigenschaften des Atomkerns

Schematische Darstellung des Atoms bzw. Atomkerns (nicht maßstabsgetreu, der untere Pfeil müsste sonst ca. 10000  mal länger sein).

Die Nukleonen: Proton und Neutron

Seit den Streuexperimenten Rutherfords wissen wir: Der Atomkern ist sehr klein, positiv geladen und vereinigt in sich fast die gesamte Masse des Atoms. Genauere Untersuchungen ergeben: Der Kerndurchmesser liegt im Bereich einiger Femtometer ($1\text{fm}=10^{-15}\text{m}$), er ist damit rund 100000 mal kleiner als das Atom. Er ist aus Nukleonen, das sind positiv geladene Protonen und elektrisch neutrale Neutronen, aufgebaut. Ein Nukleon ist dabei fast 2000 mal schwerer als ein Elektron. Zum Vergleich ist in der Tabelle neben den Nukleonen auch noch das Elektron aufgeführt:

	Proton	Neutron	Elektron
Masse	$m_p=1.6726\dots \times 10^{-27}\mathrm{k}\mathrm{g}$	$m_n=1.6749\dots \times 10^{-27}\mathrm{k}\mathrm{g}$	$m_e=9.10938\dots \times 10^{-31}\mathrm{k}\mathrm{g}$
Ladung	$q_p=1e=+1.602\dots \times 10^{-19}\mathrm{C}$	$q_n=0\mathrm{C}$	$q_e=-1e=-1.602\dots \times 10^{-19}\mathrm{C}$
Durchmesser	$r_p\sim 1.7\mathrm{f}\mathrm{m}$	$r_n\sim 1.7\mathrm{f}\mathrm{m}$	Punktförmig ($r_e<1\times 10^{-19}\mathrm{m}$)

Kerne aus Nukleonen

Der Atomkern enthält positiv geladene Protonen und elektrisch neutrale Neutronen.

Wir können nun aus den Nukleonen Atomkerne zusammensetzen. Dabei findet man, dass zur Bildung eines stabilen Atomkerns mit vorgegebener Kernladungs(an)zahl Z von Protonen ungefähr dieselbe Anzahl von Neutronen erforderlich ist. (Bei schweren Kernen sind sogar noch mehr Neutronen erforderlich). Um einen Kern anzugeben, verwendet man folgende Notation:

$\underset{A}{\overset{}{Z}}\mathrm{E}\mathrm{l}\mathrm{e}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s}\mathrm{y}\mathrm{m}\mathrm{b}\mathrm{o}\mathrm{l}$.

Dabei ist Z die Kernladungszahl (auch Ordnungszahl) und A die Massenzahl. Elementsymbol und Kernladungszahl Z sind dabei redundant, oft wird nur die Massenzahl A und das Element(symbol) angegeben. Für die Neutronenzahl N gilt damit:

$N=A-Z$.

Die chemischen Eigenschaften eines Elements sind vollkommen durch die mit der Kernladungszahl Z festgelegte Elektronenhülle vorgegeben.

Isotope

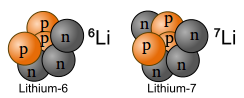
Die Anzahl der Neutronen kann für einen stabilen Kern in gewissem Rahmen variieren, d.h. von einem Element kann es verschiedene sog. Isotope geben, die sich allein durch die Anzahl N der Neutronen im Kern (und damit in der Atommasse) unterscheiden. Dieser Unterschied hat auf die chemischen Eigenschaften des jeweiligen Elements aber (fast) keinen Einfluss. In der folgenden Tabelle sind einige bekannte Isotope der einfachsten Atomsorten aufgeführt:

Name	Wasserstoff	Deuterium	Tritium	Helium	Lithium
Notation	$\underset{1}{\overset{}{1}}\mathrm{H}$	$\underset{2}{\overset{}{1}}\mathrm{H}$	$\underset{3}{\overset{}{1}}\mathrm{H}$	$\underset{4}{\overset{}{2}}\mathrm{H}\mathrm{e}$	$\underset{6}{\overset{}{3}}\mathrm{L}\mathrm{i}$	$\underset{7}{\overset{}{3}}\mathrm{L}\mathrm{i}$
Kern

Die Entdeckung Radioaktiver Strahlung

Antoine Henri Becquerel in seinem Labor.

Pierre und Marie Curie im Labor (spätestens 1906).

Die Entdeckung der Radioaktivität im ausgehenden 19. Jahrhundert durch Antoine Henri Becquerel hat in großem Maße zum Verständnis des Atoms und seines Kerns beigetragen. Sie fällt in den Zeitraum der Entdeckung von Röntgenstrahlung und ist eng mit der modernen Physik verknüpft. Es empfiehlt sich als Lektüre ein Überblick über die Entdeckung.

Eigenschaften Radioaktiver Strahlung

Ablenkung Radioaktiver Strahlung im Magnetfeld $B$. Für den Zusammenhang zwischen Bahnradius $r$ und spezifischer Ladung $\frac{q}{m}$ gilt: $\frac{q}{m}=\frac{v}{r\cdot B}$.

Alphastrahlung wird durch ein Blatt Papier, Betastrahlung durch ein Metallblech von einigen Millimeter Dicke vollständig absorbiert. Zur hinreichenden Schwächung von Gammastrahlung braucht man – je nach Energie dieser Strahlung – mehrere Zentimeter bis Dezimeter eines Materials möglichst hoher Dichte, z.B. Blei.

Mit der Entdeckung einer unbekannten Strahlung stellt sich die Frage nach ihren Eigenschaften. Wie kann man diese untersuchen?

• Reichweite, Durchdringungsvermögen → Aufschluss über mögliche Bestandteile
• Ablenkung in elektrischen/magnetischen Feldern → Aufschluss über möglich Ladung
• Energieverteilung → Erkenntnisse über Entstehungsprozesse und beteiligte Komponenten

	$\alpha$-Strahlung	$\beta$-Strahlung	$\gamma$-Strahlung
Bestandteil	${}_2^4\mathrm{H}\mathrm{e}$-Kern	Positron $e^{+}$ Elektron $e^{-}$	Elektromagnetische Strahlung, $\gamma$-Quant
Zerfallsart
Reaktion	${}_Z^A\mathrm{X}\to {}_{Z-2}^{A-4}\mathrm{Y}+{}_2^4\mathrm{H}\mathrm{e}+\mathrm{\Delta }E$	${}_Z^A\mathrm{X}\to {}_{Z-1}^A\mathrm{Y}+e^{+}\mathrm{+}{\nu }_e$ ${}_Z^A\mathrm{X}\to {}_{Z+1}^A\mathrm{Y}+e^{-}\mathrm{+}{\bar{\nu }}_e$	${}_Z^A{\mathrm{X}}^{*}\to {}_Z^A\mathrm{X}+\gamma$
Beispiel	${}_{62}^{146}\mathrm{S}\mathrm{m}\to {}_{60}^{142}\mathrm{N}\mathrm{d}+{}_2^4\mathrm{H}\mathrm{e}+2,529\mathrm{M}\mathrm{e}\mathrm{V}$	${}_{19}^{40}\mathrm{K}\to {}_{18}^{40}\mathrm{A}\mathrm{r}+e^{+}+{\nu }_e$ ${}_{79}^{198}\mathrm{A}\mathrm{u}\to {}_{80}^{198}\mathrm{H}\mathrm{g}+e^{-}+{\bar{\nu }}_e$	${}_{28}^{60}{\mathrm{N}\mathrm{i}}^{**}\to {}_{28}^{60}{\mathrm{N}\mathrm{i}}^{*}+\gamma \to {}_{28}^{60}\mathrm{N}\mathrm{i}+\gamma$
Energiespektrum
Typischer Energiebereich	2…5 MeV	Emax: einige keV bis einige MeV	~ MeV
Reichweite (Luft)	wenige Zentimeter	einige Meter	sehr weit
Abschirmung	Papier	Blech	Blei, Beton (mehrere Dezimeter), exponentielle Abschwächung
Radiotoxizität	sehr hoch	hoch	gering

Zerfallsschema von ⁶⁰Co

Detektion Radioaktiver Strahlung

Prinzip der ‚Ladungs-Lawine‘.

Funktionsprinzip des Geiger-Müller Zählers.

Datei:Nebelkammer-LMU-1.ogv

Nebelkammer mit Spur eines $\alpha$-Zerfalls.

Zerfallsgesetz, Halbwertszeit und Aktivität

Wann zerfällt ein Atomkern? Eine Aussage lässt sich nur im Rahmen von Wahrscheinlichkeiten treffen (vergl. Quantenmechanik). Für eine hinreichend große Anzahl $N$ von Kernen findet man, dass die Anzahl der Zerfälle und damit die Änderung/Abnahme $\mathrm{\Delta }N$ von $N(t)$ proportional zur Beobachtungszeit $\mathrm{\Delta }t$ und der Anzahl der vorhandenen Kerne $N(t)$ ist. Mit der Konstanten $\lambda$ können wir also schreiben:

$\mathrm{\Delta }N=-\lambda N(t)\cdot \mathrm{\Delta }t$

Diese Beziehung gilt nur für Zeiten $\mathrm{\Delta }t$, in denen sich die Anzahl $N(t)$ nicht wesentlich ändert. Dies ist in jedem Fall für infinitesimal kurze Zeiten $\mathrm{d}t$ der Fall. Wir schreiben:

$\mathrm{d}N=-\lambda N(t)\cdot \mathrm{d}t\Rightarrow \frac{\mathrm{d}N}{\mathrm{d}t}=-\lambda N(t)$.

Die Änderungsrate $\frac{\mathrm{d}N}{\mathrm{d}t}=\dot{N}(t)$ ist also proportional zur Anzahl der vorhandenen Kerne $N(t)$ und wir können die Differentialgleichung (DGL) mit dem Ansatz $N(t)=A{e}^{Bt}$, wobei $A$ und $B$ zu bestimmende Konstanten sind, lösen. Alternativ schreiben wir:

$\frac{\mathrm{d}N}{\mathrm{d}t}=-\lambda N(t)\Rightarrow \frac{\mathrm{d}N}{N}=-\lambda \cdot \mathrm{d}t$.

Wir integrieren beide Seiten vom Zeitpunkt $t_0=0$, an dem $N(0)=N_0$ Kerne vorhanden sein sollen, bis zum Zeitpunkt $t$ mit $N$ Kernen:

$\underset{N_0}{\overset{N}{\int }}\frac{\mathrm{d}N}{N}=\underset{0}{\overset{t}{\int }}-\lambda \mathrm{d}t\Rightarrow \ln (N)-\ln (N_0)=-\lambda \cdot t\Rightarrow \ln \left(\frac{N}{N_0}\right)=-\lambda \cdot t$.

Zerfallsgesetz

Die Anzahl $N(t)$ radioaktiver Atomkerne in einer gegebenen Substanzprobe nimmt exponentiell ab. Nach jedem Ablauf der Halbwertszeit $T_{1/2}$ hat sich die Anzahl der Kerne halbiert.

Für die Zerfallskonstante $\lambda$ wählen wir das Inverse einer Zeit, damit sich die Einheiten kürzen: $\lambda =\frac{1}{\tau }$. Damit erhalten wir das Zerfallsgesetz: Physik Oberstufe: Vorlage:Hervorhebung Nach der Zeit $\tau$ ist nur noch der Bruchteil $\frac{1}{e}$ der ursprünglichen Kernanzahl vorhanden.

Halbwertszeit

Die Halbwertszeit $T_{1/2}$ ist so definiert, dass nach ihrem Ablauf nur noch die Hälfte der anfangs vorhandenen $N_0$ Kerne vorhanden ist. Man findet:

$T_{1/2}=\ln (2)\cdot \tau$.

Aktivität

Als Aktivität bezeichnet man die Anzahl der Zerfälle pro Zeiteinheit: Physik Oberstufe: Vorlage:Hervorhebung

Zerfallsreihen

Nuklidkarte nach Segrè mit Angabe der radioaktiven Zerfallsart. Farbig gezeichnete Nuklide sind instabil, schwarze stabil. Die Diagonale zeigt Nuklide mit gleich vielen Protonen und Neutronen. Atomkerne mit mehr als 20 Protonen benötigen mehr Neutronen als Protonen (Neutronenüberschuss), um stabil zu sein.

Verschiedene Zerfallsarten eines Radio-Nuklids in der Nuklidkarten-Darstellung: senkrecht: Ordnungszahl (Protonenzahl) Z, waagerecht: Neutronenzahl N

Zerfällt ein instabiler Kern (Mutterkern), so ist der resultierende Tochterkern nicht notwendigerweise stabil. Ein instabiler Tochterkern zerfällt seiner Halbwertszeit entsprechend ebenfalls. So entsteht eine Zerfallsreihe, eine Kette von aufeinander folgenden Zerfällen, die erst bei einem stabilen Kern endet. Aus der Nuklidkarte kann man bei gegebenem Mutterkern die Zerfallskette konstruieren.

Massendefekt

Gedankenexperiment: Wir setzen einen $\underset{4}{\overset{}{2}}\mathrm{H}\mathrm{e}$-Kern aus Neutronen und Protonen zusammen und berechnen seine Masse:

$2\cdot m_p+2\cdot m_n=2\cdot 1.6726\times 10^{-27}\mathrm{k}\mathrm{g}+2\cdot 1.6749\times 10^{-27}\mathrm{k}\mathrm{g}=6.695\times 10^{-27}\mathrm{k}\mathrm{g}$.

Atomkernbindungsenergie RK01

Binding energy curve - common isotopes DE

Vergleichen wir die aus den Komponenten berechnete Masse mit der gemessenen Masse $m_{{}^4{}_2\mathrm{H}\mathrm{e}}=6.644657\dots \times 10^{-27}\mathrm{k}\mathrm{g}$ eines $\alpha$-Teilchens, also eines $\underset{4}{\overset{}{2}}\mathrm{H}\mathrm{e}$-Kerns, so beobachten wir einen Massenverlust, den sog. Massendefekt $\mathrm{\Delta }m$:

$\mathrm{\Delta }{m}_{{}^4{}_2\mathrm{H}\mathrm{e}}:=2\cdot m_p+2\cdot m_n-m_{{}^4{}_2\mathrm{H}\mathrm{e}}\approx 0.05\times 10^{-27}\mathrm{k}\mathrm{g}$.

Eine Erklärung dieses Massendefekts liefert die Spezielle Relativitätstheorie mit der Äquivalenz von Masse und Energie: In einem abgeschlossenen System ist nicht notwendigerweise die Masse konstant, wohl aber die Energie, wenn man Ruhemassen $m_0$ gemäß der Formel $E=m_0{c}^2$ berücksichtigt. Offensichtlich hat der $\underset{4}{\overset{}{2}}\mathrm{H}\mathrm{e}$-Kern eine geringere Energie als die einzelnen Bestandteile, und zwar:

$\mathrm{\Delta }E=\mathrm{\Delta }{m}_{{}^4{}_2\mathrm{H}\mathrm{e}}{c}^2\approx 4.5\times 10^{-12}\mathrm{J}\approx 28\mathrm{M}\mathrm{e}\mathrm{V}$.

Pro Nukleon werden also bei der Bildung des Kerns ca. $7\mathrm{M}\mathrm{e}\mathrm{V}$ Energie frei. Umgekehrt ist diese Energie (pro Nukleon) nötig, um den Kern wieder in seine Bestandteile zu zerlegen. Man bezeichnet $\mathrm{\Delta }E$ darum auch als Bindungsenergie des Kerns.

Kernreaktionen

Kernspaltung

Spaltung eines Uran-235 Kerns.

Wirkungsquerschnitt für die Spaltungsreaktion von U-233, U-235, U-238 und Pu-239 in Abhängigkeit der Neutronenernergie. Der linke Bereich entspricht thermischen d.h. langsamen, der rechte schnellen Neutronen.

Kernspaltungs-Kettenreaktion.

Lise Meitner et. al

${}_{92}^{235}\mathrm{U}+{}_0^1\mathrm{n}\to {}_{56}^{139}\mathrm{B}\mathrm{a}+{}_{36}^{95}\mathrm{K}\mathrm{r}+2{}_0^1\mathrm{n}$