Mathe für Nicht-Freaks: Mittelwertsatz für Integrale

{{#invoke:Mathe für Nicht-Freaks/Seite|oben}}

Nach dem Mittelwertsatz für Integrale nehmen stetige Funktionen auf einem kompakten Intervall ihren durchschnittlichen Wert an. Dieser Satz kann unter anderem zum Beweis des Hauptsatzes der Differential- und Integralrechnung verwendet werden. Dieser stellt einen Zusammenhang zwischen Integral und Ableitung her.

Das Integral als Durchschnittswert

Wiederholung: Durchschnitt und gewichteter Durchschnitt

Mit dem Integral kann der Durchschnittswert einer Funktion bestimmt werden. Bei $n$ verschiedenen Werten $y_1$ bis $y_n$ kann ihr Durchschnitt bzw. der Mittelwert $\bar{y}$ bestimmt werden über

So ist der Durchschnitt der Werte $(1,1,2,3)$ gleich $\frac{1}{4}(1+1+2+3)=\frac{7}{4}$. Wenn die einzelnen Werte $y_1$ bis $y_n$ in der Berechnung des Durchschnitts durch unterschiedliche Faktoren $w_1$ bis $w_n$ gewichtet werden sollen, lautet die Formel:

Eine Gewichtung $w_i=2$ bedeutet beispielsweise, dass der Wert $y_i$ doppelt so stark in den Durchschnitt eingehen soll, als wenn $w_i=1$ wäre.

Durchschnittsberechnung einer Funktion

Eine Funktion $f:[a,b]\to ℝ$ hat unendlich viele Argumente und nimmt damit unendlich oft Funktionswerte an. Die Formel zur Mittelwertsberechnung von endlich vielen Werten kann also nicht verwendet werden, um den durchschnittlichen Funktionswert von $f$ zu bestimmen. Wir können diesen aber annähern. Hierzu zerlegen wir das Intervall $[a,b]$ in Teilintervalle. Durch die Wahl von Stützstellen $(x_0,x_1,\dots ,x_n)$ mit $x_0=a$ und $x_n=b$ wird das Intervall $[a,b]$ in $n$ Intervalle $[x_{k-1},x_k]$ mit $1\le k\le n$ unterteilt:

Zerlegung des Grundintervalls in zehn Teilintervalle

Sei nun $M_{k,n}$ das Supremum und $m_{k,n}$ das Infimum der Funktionswerte von $f$ im Teilintervall $[x_{k-1},x_k]$. Damit das Supremum und Infimum existiert, nehmen wir zusätzlich an, dass $f$ beschränkt ist. Nun können zwei Treppenfunktionen definiert werden, die jeweils die Funktion $f$ von oben bzw. von unten annähern. Bei der oberen Treppenfunktion $T:[a,b]\to ℝ$ definieren wir $T(x)=M_{k,n}$ für $x\in [x_{k-1},x_k)$ und $T(x_n)=f(x_n)$. Bei der unteren Treppenfunktion $t:[a,b]\to ℝ$ ist $t(x)=m_{k,n}$ bei $x\in [x_{k-1},x_k)$ und $t(x_n)=f(x_n)$:

• 
  Treppenfunktion $t$, die die Funktion von unten approximiert.
• 
  Treppenfunktion $T$, die die Funktion von oben approximiert.

Beide Treppenfunktionen nehmen nur endlich viele Werte an und nähern beide den Funktionsverlauf von $f$ an. Da die Werte von $T$ immer über den Werten von $f$ liegen, sollte auch der durchschnittliche Wert von $T$ größer gleich dem Mittelwert von $f$ sein. Der Durchschnittswert der oberen Treppenfunktion schätzt also den gesuchten Funktionsmittelwert nach oben ab. Analog ist der Durchschnittswert der unteren Treppenfunktion eine Abschätzung nach unten für den Mittelwert von $f$.

Um den Mittelwert einer Treppenfunktion zu bestimmen, reicht es nicht aus, den Durchschnitt der angenommenen Funktionswerte zu bilden. So nehmen die folgenden Treppenfunktionen dieselben Funktionswerte an. Wegen der unterschiedlichen Größe der Teilintervalle sollte sich aber der Durchschnittswert der beiden Teilintervalle unterscheiden:

• 
  Treppenfunktion mit den Werten $0$, $1$ und $2$. Der durchschnittliche Wert sollte aber größer als $\frac{1}{3}(0+1+2)=1$ sein.
• 
  Auch diese Treppenfunktion nimmt nur die Werte $0$, $1$ und $2$ an. Ihr durchschnittlicher Wert sollte aber geringer als $1$ sein.

Vielmehr müssen wir die Funktionswerte mit den Längen der Teilintervalle an der Stelle gewichten, wo diese Funktionswerte angenommen werden. Das $k$-te Teilintervall $[x_{k-1},x_k]$ hat die Länge $x_k-x_{k-1}$. Bei der oberen Treppenfunktion $T$ bilden wir also den Mittelwert $\bar{T}$ der Zahlen $M_{k,n}$ mit den Gewichten $x_k-x_{k-1}$:

Analog können wir den Durchschnittswert $\bar{t}$ der unteren Treppenfunktion bestimmen. Insgesamt erhalten wir die Abschätzung:

Wir konnten also den durchschnittlichen Funktionswert $\bar{f}$ der gegebenen Funktion $f$ abschätzen. Als Summen treten dabei die Ober- und Untersummen auf, die selbst den orientierten Flächeninhalt unter dem Graphen approximieren. Um die obige Abschätzung weiter zu verbessern, müssen wir das Grundintervall immer feiner zerlegen. Unter der Voraussetzung, dass die Funktion $f$ riemannintegrierbar ist, strebt dabei die Unter- sowie die Obersumme gegen das Integral $\underset{a}{\overset{b}{\int }}f(x)\mathrm{d}x$. Mit Hilfe des Sandwichsatzes können wir aus obiger Abschätzung folgern:

Mit Hilfe des Integrals kann also der Durchschnittswert einer Funktion bestimmt werden. Hierzu muss das Integral durch die Länge $b-a$ des Grundintervalls geteilt werden.

Geometrische Herleitung

Der Zusammenhang zwischen Integral und Mittelwert einer Funktion $f:[a,b]\to ℝ$ kann geometrisch hergeleitet werden. Betrachten wir hierzu eine integrierbare Funktion $f:[a,b]\to ℝ$. Das Integral ${\int }_a^{b}f(x)\mathrm{d}x$ entspricht dem orientiertem Flächeninhalt zwischen dem Graphen von $f$ und der $x$-Achse:

Das Integral entspricht der orientierten Fläche unterhalb des Funktionsgraphen

Wenn wir die Funktion so verändern, dass sie nur den durchschnittlichen Funktionswert annimmt, dann sollte sich ihr Flächeninhalt unter dem Graphen nicht ändern. Wir können den Durchschnittswert $\bar{f}$ der Funktion $f$ also darüber definieren, dass der Flächeninhalt des Rechtecks mit der Grundseite $[a,b]$ auf der $x$-Achse und der Höhe $\bar{f}$ gleich dem orientierten Flächeninhalt unter dem Graphen von $f$ ist:

Der Flächeninhalt unter dem Graphen der Funktion, die nur den durchschnittlichen Funktionswert annimmt, ist gleich dem Flächeninhalt unter dem Graphen der ursprünglichen Funktion

Damit erhalten wir die Gleichung $\bar{f}\cdot (b-a)={\int }_a^{b}f(x)\mathrm{d}x$. Diese können wir umformen zu:

Der Mittelwertsatz

Bedeutung

Gibt es ein Argument $\xi \in [a,b]$, so dass $f(\xi )$ dem durchschnittlichen Wert von $f$ entspricht? Dies ist die zentrale Frage hinter dem Mittelwertsatz für Integrale

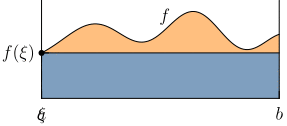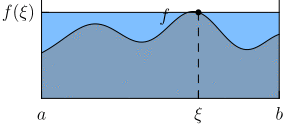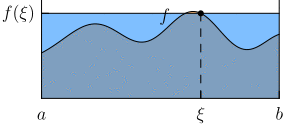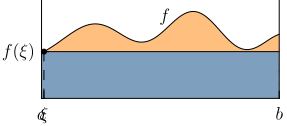
Bei einer stetigen Funktion $f:[a,b]\to ℝ$ liegt der Durchschnittswert im Bereich der Werte, welche die Funktion annimmt. Es gibt also ein $\xi$, so dass $f(\xi )$ gleich dem durchschnittlichen Funktionswert von $f$ ist. Das Rechteck mit der Breite $b-a$ und der Höhe $f(\xi )$ besitzt dann denselben Flächeninhalt wie die Funktion $f$ unter ihrem Graphen:

Annäherung des Integrals durch ein Rechteck

Dies ist bereits die Aussage des Mittelwertsatzes: Eine stetige Funktion nimmt ihren Mittelwert als Funktionswert an. Es gibt also für alle stetigen Funktionen $f:[a,b]\to ℝ$ mindestens ein Argument $\xi \in [a,b]$ mit:

Um auch den Fall $a=b$ zu erlauben, stellen wir obige Gleichung um und erhalten so ein $\xi \in [a,b]$ mit:

Notwendigkeit der Stetigkeitsvoraussetzung

Dass der Mittelwertsatz für Integrale nicht für beliebige Funktionen gilt und dass die Stetigkeit als Voraussetzung wichtig ist, zeigt die Funktion $g:[0,2]\to ℝ$ mit

Diese Funktion ist riemannintegrierbar, weil sie aus zwei konstanten Funktionen zusammengesetzt ist. Es gilt

Der durchschnittliche Funktionswert beträgt also

Nach Betrachtung des Funktionsverlaufs macht dies auch Sinn. Allerdings wird der Wert $\frac{1}{2}$ von $g$ nicht angenommen, da $0$ und $1$ die einzigen Funktionswerte sind. Bei unstetigen Funktion wie $g$ ($g$ ist an der Stelle $1$ unstetig) ist der Mittelwertsatz nicht unbedingt erfüllt.

Verallgemeinerter Mittelwertsatz

Motivation

Es gibt auch eine verallgemeinerte Variante des Mittelwertsatzes für Integrale. Dabei wird zusätzlich zu unserer Funktion $f:[a,b]\to ℝ$ noch eine Gewichtungsfunktion $g:[a,b]\to ℝ$ eingeführt, die beschreibt, wie stark die einzelnen Funktionswerte bei der Berechnung des Durchschnittswerts ins Gewicht fallen sollen.

Ein solches gewichtetes Mittel ist dir vielleicht bereits vom Durchschnitt endlich vieler Zahlen bekannt. Wollen wir etwa den Durchschnitt der Zahlen $2,3,7$ ermitteln und dabei die $2$ und die $7$ jeweils doppelt so stark wie die $3$ zählen lassen, so berechnen wir Vorlage:Einrücken Wir multiplizieren also jede Zahl mit ihrer Gewichtung und teilen die Summe davon anschließend durch die Summe der Gewichte.

Dies übertragen wir nun auf den gewichteten Durchschnittswert von Funktionen und erhalten Vorlage:Einrücken als den Mittelwert von $f$ bezüglich der Gewichtungsfunktion $g$.

Der verallgemeinerte Mittelwertsatz für Integrale besagt nun, dass auch dieser gewichtete Mittelwert als Funktionswert vorkommt. Es gibt also ein $\xi \in [a,b]$ mit Vorlage:Einrücken beziehungsweise Vorlage:Einrücken Im Folgenden werden wir die letztere Schreibweise verwenden, da diese auch im Fall ${\int }_a^{b}g(x)\mathrm{d}x=0$ gültig bleibt.

Die Aussage des Satzes stimmt allgemein jedoch nur, wenn die Gewichtungsfunktion niemals negativ wird, also $g(x)\ge 0$ für alle $x\in [a,b]$ gilt. Anschaulich macht es auch wenig Sinn, gewisse Funktionswerte negativ ins Gewicht fallen zu lassen.

Die Gewichtungsfunktion $g$ muss im Gegensatz zu $f$ nicht unbedingt stetig sein. Es ist nur wichtig, dass $g$ riemannintegrierbar ist, damit die Integrale ${\int }_a^{b}f(x)g(x)\mathrm{d}x$ und ${\int }_a^{b}g(x)\mathrm{d}x$ überhaupt existieren.

Ursprünglicher Mittelwertsatz als Spezialfall

Wenn wir im verallgemeinerten Mittelwertsatz die konstante Gewichtungsfunktion $g(x)=1$ ($x\in [a,b]$) wählen, so bekommen wir den ursprünglichen Mittelwertsatz zurück, denn dann ist Vorlage:Einrücken sowie Vorlage:Einrücken

Notwendigkeit von $g\ge 0$

Die Bedingung $g\ge 0$ kann nicht weggelassen werden, wie folgendes Gegenbeispiel zeigt:

Man kann die Bedingung $g\ge 0$ jedoch ersetzen durch die Bedingung $g\le 0$. Es lässt sich beweisen, dass der verallgemeinerte Mittelwertsatz dann weiterhin gültig ist. Es ist nur wichtig, dass die Gewichtungsfunktion $g$ keinen Vorzeichenwechsel besitzt.

{{#invoke:Mathe für Nicht-Freaks/Seite|unten}}