Physik Oberstufe/ Schwingungen und Wellen/ Mechanische Wellen: Unterschied zwischen den Versionen
imported>Rumil K Gestaltung gegen Vorlagen ersetzt. |
(kein Unterschied)
|
Aktuelle Version vom 26. März 2017, 09:12 Uhr
Grundbegriffe

Physik Oberstufe: Vorlage:Experiment-Box
Eindimensionale harmonische Wellen


Betrachten wir die eindimensionale Welle (Bild). Die Welle breitet sich mit der Ausbreitungsgeschwindigkeit aus. Davon zu unterscheiden ist die Geschwindigkeit jedes einzelnen Massenpunktes, die man als Schnelle bezeichnet.
Jeder Massepunkt macht eine harmonische Schwingung in vertikaler Richtung. Mit der Frequenz bzw. der Periodendauer dieser Schwingung folgt die wichtige Beziehung: Physik Oberstufe: Vorlage:Hervorhebung
Mathematische Beschreibung harmonischer Wellen
Wir wollen die Welle durch eine von Ort und Zeit abhängige Funktion beschreiben:
Die Masse an der Stelle schwinge nach der Gleichung:
Dann schwingt eine Masse an der Stelle gemäß:
mit der von abhängigen Phasenverschiebung . Die Funktion muss linear mit den folgenden Eigenschaften sein:
Damit folgt: Physik Oberstufe: Vorlage:Hervorhebung
Beschreibung mit Zeigern

Harmonische Wellen an festem Ort oder zu fester Zeit können mit rotierenden Zeigern beschrieben werden. Wie aus dem Bild ersichtlich, entspricht eine Periode an festem Ort einer Rotation des Zeigers um . Das selbe gilt bei festgehaltener Zeit für eine Wellenlänge. Diese Beschreibung ist insbesondere bei der Überlagerung von Wellen vorteilhaft (siehe unten).
Longitudinale und transversale Wellen

Man unterscheidet zwei grundsätzliche Wellenarten:
Transversale Wellen (Querwellen)
- Die Auslenkung/Schnelle steht senkrecht auf der Ausbreitungsrichtung:
- Beispiele/Darstellungen von Transversalwellen
Longitudinale Wellen (Längswellen)
- Die Auslenkung/Schnelle erfolgt parallel zur Ausbreitungsrichtung:
- Beispiele/Darstellungen von Longitudinalwellen
Überlagerung von Wellen

Überlagern sich zwei gegeneinander laufende Wellenberge exakt, so entsteht ein Zustand, bei dem die Schnelle der resultierende Welle überall verschwindet.
Überlagern sich zwei gegeneinander laufende Wellen, Berg und entsprechendes Tal, so verschwindet für einen Moment die Auslenkung überall.
Physik Oberstufe: Vorlage:Experiment-Box
Spezialfälle
Ein nach rechts laufender Wellenberg trifft auf einen identischen, nach links laufenden Wellenberg. Im Moment der vollständigen Überlagerung:
- entsteht ein Wellenberg doppelter Auslenkung,
- ist die Schnelle überall identisch Null.
Ein nach rechts laufender Wellenberg trifft auf ein entsprechendes, nach links laufendes Wellental. Im Moment der vollständigen Überlagerung:
- entsteht ein Zustand ohne jede Auslenkung,
- verdoppelt sich die Schnelle.
Interferenzprinzip
Physik Oberstufe: Vorlage:Hervorhebung
Schwebung
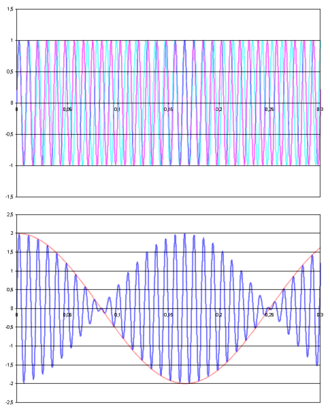

Physik Oberstufe: Vorlage:Experiment-Box
Stehende Wellen
Physik Oberstufe: Vorlage:Experiment-Box
Reflexion von Wellen
Physik Oberstufe: Vorlage:Experiment-Box
Stehende Wellen durch Reflexion

Wenn wir statt eines einzelnen Wellenbergs eine kontinuierliche, harmonische Welle auf dem Wellenträger starten, so wird diese ebenfalls am Ende reflektiert:
- Am losen Ende hat die reflektierte Welle die gleiche Phase wie die einlaufende Welle. Durch Überlagerung der einlaufenden mit der reflektierten Welle bildet sich eine stehende Welle mit einem Schwingungsbauch am losen Ende des Wellenträgers.
- Am festen Ende hat die reflektierte Welle eine Phasenverschiebung um relativ zur einlaufenden Welle. Man spricht von einem Phasensprung um am festen Ende. Wieder bildet sich eine stehende Welle, diesmal mit einem Knoten am festen Ende.
Physik Oberstufe: Vorlage:Experiment-Box
Eigenschwingungen (Eigenmoden)



Wir betrachten nun einen eindimensionalen, in beiden Richtungen begrenzten Wellenträger der Länge .
Zwei feste Enden
Typisches Beispiel ist die gespannte Saite eines Musikinstruments. Man beobachtet stehende Wellen unterschiedlicher Wellenlänge, die stets einen Knoten an den Enden vorweisen. Für die Grundschwingung, die Schwingung mit der kleinsten bzw. tiefsten Frequenz, findet man mit :
- .
Die nächste mögliche stehende Welle, die die Bedingung der Knoten an den Enden erfüllt, ist die erste Oberschwingung. Dabei passt genau eine Wellenlänge auf den Wellenträger und es gilt:
- .
In der Akustik entspricht dieser Frequenzunterschied einer Oktave. Für die zweite Oberschwingung gilt entsprechend:
- .
Ein festes und ein loses Ende
Der Fall eines festen und eines losen Endes liegt u.a. bei vielen Blasinstrumenten und Pfeifen vor. Für die Grundschwingung gilt:
- ,
für die ersten beiden Oberschwingungen:
- und
|
Aufgabe |
Physik Oberstufe: Vorlage:Hervorhebung-ohne-Einzug






