Physik Oberstufe/ Schwingungen und Wellen/ Elektromagnetische Schwingungen

< Mechanische Schwingungen | Inhaltsverzeichnis | Mechanische Wellen >

Die elektromagnetische Schwingung

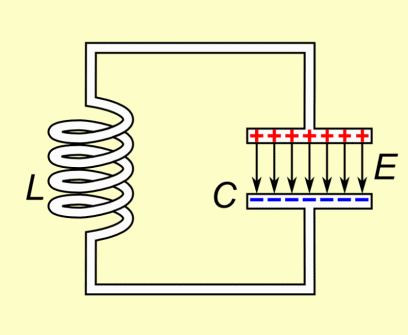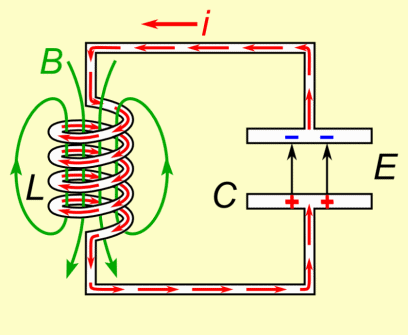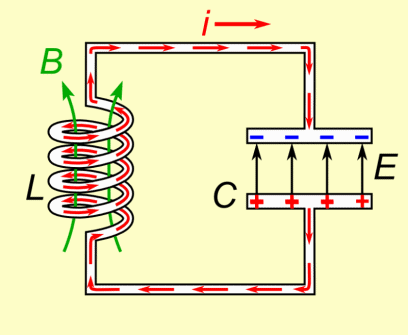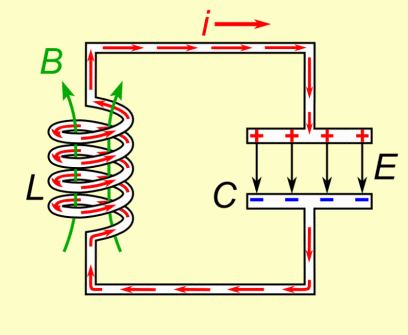
Animation eines elektrischen Schwingkreises. Periodisch wird Energie des elektrischen Feldes in Energie des magnetischen Feldes und umgekehrt umgewandelt.

Physik Oberstufe: Vorlage:Experiment-Box Physik Oberstufe: Vorlage:Hervorhebung

Mathematische Beschreibung der elektromagnetischen Schwingung

LC-Schwingkreis: Zum Zeitpunkt $t = 0$ wird der Kondensator $C$ über die Induktivität $L$ entladen.

Durch Anwendung der Maschenregel im Schwingkreis erhält man:

0 = U_{C} + U_{L} .

$U_{C}$ und $U_{L}$ sind nicht unabhängig voneinander. Es bietet sich an, die Spannungen über die Ladung bzw. die Änderung des Stromes auszudrücken:

U_{C} = \frac{Q}{C} und U_{L} = L \cdot \dot{I} .

Eingesetzt ergibt sich:

\frac{Q}{C} + L \cdot \dot{I} = 0 .

Bestimmung der Ladung $Q (t)$

Zwischen der Ladung $Q$ und dem Strom $I$ besteht ein Zusammenhang. Fließt ein Strom, so ändert sich die Ladung auf den Kondensatorplatten. Umgekehrt hat jede Änderung der Kondensatorladung einen Stromfluss zu Folge. Bei unserer Definition der Stromrichtung bewirkt ein positiver Strom ein Anwachsen der Ladung auf den Kondensatorplatten. Die Definition der elektrischen Stromstärke selbst:

I : = \frac{Δ Q}{Δ t}

müssen wir, da sich die fließende Ladung permanent ändert, für infinitesimal kleine Zeitintervalle $Δ t$ auswerten. Mathematisch wird aus dem Differenzenquotient der Differentialquotient:

I (t) : = \frac{d Q (t)}{d t} = Q^{'} (t) = \dot{Q} ⟹ \dot{I} (t) = \ddot{Q} (t)

In unsere Gleichung eingesetzt erhalten wir:

\frac{Q}{C} + L \cdot \ddot{Q} = 0 \Rightarrow

Physik Oberstufe: Vorlage:Hervorhebung Diese Differentialgleichung kennen wir bereits vom harmonischen Oszillator: Gesucht ist eine Funktion $Q (t)$ , die zwei mal abgeleitet bis auf den Faktor $\frac{- 1}{L C}$ sich selbst ergibt. Wir können wieder einen entsprechenden Ansatz machen, oder die Konstanten der beim harmonischen Oszillator gefundene Lösung entsprechend anpassen. Man findet die allgemeine Lösung der Differentialgleichung des elektrischen Schwingkreises: Physik Oberstufe: Vorlage:Hervorhebung Die maximale Ladung $\hat{Q}$ und die Phase $φ$ sind Integrationskonstanten, die durch die Anfangsbedingungen definiert werden.