Physik Oberstufe/ Elektrizitätslehre/ Das elektrische Feld

Die Wechselwirkung elektrischer Ladungen

Schaltkreis, Blick in den Leiter: Atomrümpfe sind fest, es bewegen sich die Elektronen. Physik Oberstufe: Vorlage:Experiment-Box

Beschreibung durch Felder

Eine Ladung $Q$ übt auf kleine Probeladungen $q$ Kräfte aus. Während das resultierende Kraftfeld auch von der Probeladung $q$ abhängt, wird das elektrische Feld $\overrightarrow{E}$ nur noch durch die „felderzeugende Ladung“ $Q$ bestimmt.

Man bezeichnet physikalische Größen, die an jedem Ort $(x,y,z)$ im Raum definiert sind, als Felder.

Beispiele:

• Temperaturfeld $T(x,y,z)$
• Strömungsfeld: Windrichtung und -geschwindigkeit, Geschwindigkeitsfeld $\overrightarrow{v}(x,y,z)$
• Kraftfeld $\overrightarrow{F}(x,y,z)$

Hier: Eine große Ladungsmenge $Q$ übt auf die kleine Probeladung $q$ eine Kraft aus: Problem: Das Kraftfeld hängt auch von der Größe der Probeladung $q$ ab.

Lösung: Wir definieren das elektrische Feld Feld$\overrightarrow{E}$ als: Physik Oberstufe: Vorlage:Hervorhebung Dabei ist ${\overrightarrow{F}}_{\mathrm{e}\mathrm{l}}$ die Kraft auf die Probeladung $q$ am Ort $(x,y,z)$. Das elektrische Feld der Ladung $Q$ hängt nur von der Ladung $Q$ selbst ab und hat die Richtung der Kraft auf eine positive Probeladung.

Für die Einheit des elektrischen Feldes gilt:

$[E]=\frac{\mathrm{N}}{\mathrm{C}}=\frac{\mathrm{V}}{\mathrm{m}}$.

Superpositionsprinzip, Feld- und Äquipotentiallinien

Superpositionsprinzip

Superpositionsprinzip: Das resultierende Feld mehrere Ladungen ergibt sich aus der Summe aller Felder der einzelnen Ladungen: $\overrightarrow{E}={\overrightarrow{E}}_1+{\overrightarrow{E}}_2$ → statische Grafik

Um an einem Ort das elektrische Feld einer Ladungsverteilung zu ermitteln, wenden wir das Superpositionsprinzip an. Es besagt, dass sich das resultierende Feld ${\overrightarrow{E}}_{\mathrm{r}\mathrm{e}\mathrm{s}}$ mehrerer Ladungen aus der Summe der Felder der einzelnen Ladungen ergibt:

${\overrightarrow{E}}_{\mathrm{r}\mathrm{e}\mathrm{s}}={\overrightarrow{E}}_1+{\overrightarrow{E}}_2+\dots =\sum _k{\overrightarrow{E}}_k.$

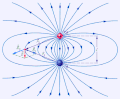
Elektrische Feldlinien

Wir verwenden Feld- und Äquipotentiallinien um elektrische Felder zu veranschaulichen.

Feld einer positiv geladenen Kugel.

Feld einer negativ geladenen Kugel.

Feld zweier verschiedennamig geladenen Kugeln.

In der Elektrostatik gelten für elektrische Feldlinien die folgenden Regeln:

• Feldlinien verlaufen von positiven zu negativen Ladungen ⇒ es gibt keine geschlossenen Feldlinien.
• Feldlinien schneiden sich nie (es gibt nur eine Richtung der resultierenden Kraft auf eine Probeladung).
• Je dichter die Feldlinien, desto größer die Feldstärke.
• Feldlinien stehen stets senkrecht auf leitenden Oberflächen.

• 
• 
• 
• 
• 
• 

Elektrische Leiter im Feld

Feld einer geladenen Kugel vor einer geerdeten, leitenden Kugel.

Feld einer geladenen Kugel vor einer neutralen, leitenden Kugel.

Feld einer geladenen Kugel vor einer leitenden Platte.

Animation zum Faradayschen Käfig.

Elektrische Leiter zeichnen sich dadurch aus, dass in ihnen frei bewegliche Ladungen vorliegen. Im elektrischen Feld verschieben sich die Ladungen (Influenz) so lange, bis im Leiter kein elektrisches Feld mehr existiert, das Innere von Leitern ist also feldfrei und aufgebrachte Ladung sitzt an der Oberfläche. Diese Oberfläche hat überall das selbe Potential, ist also Äquipotentialfläche.

Äquipotentiallinien

Äquipotentiallinien (rot) und Feldlinien (schwarz) für zwei punktförmig konzentrierte Ladungen gleichen Vorzeichens

Elektrisches Feld und Äquipotentiallinien im Plattenkondensator.

Neben Feldlinien kann man Äquipotentiallinien zur Beschreibung von Feldern verwenden. Es gelten die folgenden Regeln:

• Äquipotentiallinien stehen immer senkrecht auf Feldlinien.
• Ladungen können auf Äquipotentiallinien ohne Kraftaufwand verschoben werden.

---

Aufgabe: Simulation: Feld- und Äquipotentiallinien.

---

Feldmessung Plattenkondensator

Feld eines Plattenkondensators. Im Inneren der Platten liegt ein homogenes Feld vor. Außerhalb fällt das Feld schnell ab.

ToDo: Direkte Messung der Ladung auf der Kugel und indirekt über den fließenden Strom bei zwischen den Platten pendelnder Kugel.

Das elektrische Feld im Plattenkondensator

Aus der Definition der Spannung:

$U:=\frac{W}{q}⟹W=U\cdot q$

können wir eine Formel für das homogene Feld im Plattenkondensator herleiten. Für die erforderliche Arbeit $W$, um eine Ladung $q$ von einer Kondensatorplatte zur anderen zu transportieren, erhalten wir mit dem Plattenabstand $d$:

$W=F_{\mathrm{e}\mathrm{l}}\cdot d=E\cdot q\cdot d.$

Einsetzen der Beziehung für $W$ ergibt:

$U\cdot q=E\cdot q\cdot d,$

und damit gilt für das homogene Feld im Plattenkondensator: Physik Oberstufe: Vorlage:Hervorhebung

Beschleunigung von Ladungen im elektrischen Feld

Die Kraft ${\overrightarrow{F}}_{\mathrm{e}\mathrm{l}}=\overrightarrow{E}\cdot q$ auf Ladungen im elektrischen Feld $\overrightarrow{E}$ beschleunigt frei bewegliche, geladene Teilchen. Mit der kinetischen Energie $W_{\mathrm{k}\mathrm{i}\mathrm{n}}=\frac{1}{2}m{v}^2$ und der Definition der Spannung $U:=\frac{W}{q}$ erhält man unter Benutzung des Energieerhaltungssatzes:

$W_{\mathrm{p}\mathrm{o}\mathrm{t}}=U\cdot q=W_{\mathrm{k}\mathrm{i}\mathrm{n}}=\frac{1}{2}m{v}^2$

$⟹v=\sqrt{\frac{2qU}{m}}$

Anwendung: Braunsche Röhre

Schematischer Aufbau einer Braunschen Röhre. Um möglichst viele Elektronen auf die Blendenöffnung zu fokussieren, verwendet man zwischen Kathode und Anode weitere feldformende Elemente wie den sog. Wehneltzylinder.

Elektronenkanone mit Wehneltzylinder:
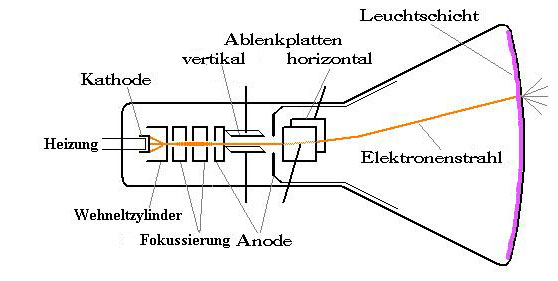
➀ Glühkathode, ➁ Wehneltzylinder, ➂ Anodenblende.

Elektronenkanone

Mit einer Elektronenkanone kann man einen Elektronenstrahl erzeugen. Sie besteht im Wesentlichen aus einer Glühkathode und einer mit einem Loch versehenen Anodenplatte. Damit Elektronen aus der Kathode austreten (Edison-Richardson/glühelektrischer Effekt), erhitzt man diese über eine Glühwendel oder verwendet die Glühwendel selbst als Kathode. Durch die zwischen Kathode und Anode angelegte Beschleunigungsspannung $U_{\mathrm{A}}$ werden die negativ geladenen Elektronen entgegen der Feldrichtung beschleunigt. Ein Großteil prallt auf die Anode, einige Elektronen passieren jedoch die Anode durch das Loch und bewegen sich anschließend im näherungsweise feldfreien Raum mit der Geschwindigkeit ${\overrightarrow{v}}_x$weiter. Um möglichst viele Elektronen auf die Blendenöffnung zu fokussieren, verwendet man zwischen Kathode und Anode weitere feldformende Elemente wie den sog. Wehneltzylinder.

Strahlgeschwindigkeit $v_x$

Mit obiger Überlegung erhält man bei einer Beschleunigungsspannung $U_{\mathrm{A}}$ für die Geschwindigkeit $v_x$ der Elektronen im Strahl:

$v_x=\sqrt{\frac{2e{U}_{\mathrm{A}}}{m_e}}.$

Dabei ist $e=1.602\dots \times 10^{-19}\mathrm{C}$ die Elementarladung (der Betrag der Ladung des Elektrons) und $m_e=9.109\dots \times 10^{-31}\mathrm{k}\mathrm{g}$ die Masse des Elektrons.

Ablenkung des Strahls

Braunsche Röhre: ① Glühkathode, ② Wehneltzylinder, ③ Anode, ④ Ablenkkondensator und ⑤ Leuchtschicht.

Animation einer Braunschen Röhre, die Lissajous-Figuren zeigt.

Der Elektronenstrahl kann durch Ablenkkondensatoren, die senkrecht zum ursprünglichen Strahl angeordnet sind, abgelenkt werden. Da die Kraft ${\overrightarrow{F}}_{\mathrm{e}\mathrm{l}}$ im Feld des Ablenkkondensators senkrecht auf der Geschwindigkeit ${\overrightarrow{v}}_x$ steht, ändert sich diese Geschwindigkeitskomponente nicht. Verläuft das Feld beispielsweise in $y$-Richtung, wird nur die Geschwindigkeitskomponente $v_y$ beeinflusst. Dies ist analog zum waagerechten Wurf im Gravitationsfeld. Während die Komponente $v_x$ unverändert bleibt, führt das Elektron in $y$-Richtung eine gleichmäßig beschleunigte Bewegung aus.

Für eine gleichmäßig beschleunigte Bewegung aus der Ruhe gelten die bekannten Zusammenhänge:

$v=a\cdot t$ und $s=\frac{1}{2}a\cdot t^2$.

Nun setzen wir für die Beschleunigung $a$:

$a=\frac{F_{\mathrm{e}\mathrm{l}}}{m_e}=\frac{e\cdot E_C}{m_e}=\frac{e\cdot U_C}{d\cdot m_e}$.

Wobei wir die Definition des elektrischen Feldes $\overrightarrow{E}:=\frac{{\overrightarrow{F}}_{\mathrm{e}\mathrm{l}}}{q}$ und die Feldstärke im Plattenkondensator (Plattenabstand $d$) $E_C=\frac{U_C}{d}$ verwendet haben. Die Zeit $t$ können wir mit $v_x$ durch die Position $x$ im Kondensator ausdrücken $t=\frac{x}{v_x}$.

Geschwindigkeit $v_y$ im Kondensator

Für die Geschwindigkeit $v_y$ im Kondensator erhalten wir:

$v_y=\frac{e\cdot U_C}{d\cdot m_e}\cdot \frac{x}{v_x}$.

Setzen wir nun noch $v_x$ von oben ein, erhalten wir:

$v_y=\frac{e\cdot U_C}{d\cdot m_e}\cdot \frac{\sqrt{m_e}}{\sqrt{2e{U}_{\mathrm{A}}}}\cdot x=\sqrt{\frac{e}{2m_e{U}_{\mathrm{A}}}}\cdot \frac{U_C}{d}\cdot x$

Hat der Kondensator die Länge $l$, so beträgt nach dem Kondensator die Geschwindigkeit der Elektronen in $y$-Richtung:

$v_y=v_l=\sqrt{\frac{e}{2m_e{U}_{\mathrm{A}}}}\cdot \frac{U_C}{d}\cdot l$.

Ort $y$ im Kondenator

Für den Ort $y$ im Kondensator erhalten wir:

$y=\frac{e\cdot U_C}{2\cdot d\cdot m_e}\cdot \frac{x^2}{v_x^2}$.

Setzen wir nun wieder $v_x$ ein, ergibt sich:

$y=\frac{e\cdot U_C}{2\cdot d\cdot m_e}\cdot \frac{m_e}{2e{U}_{\mathrm{A}}}\cdot x^2=\frac{U_C}{4\cdot d\cdot U_{\mathrm{A}}}\cdot x^2$.

Am Ende des Kondensators haben die Elektronen die $y$-Position:

$y_l=\frac{U_C}{4\cdot d\cdot U_{\mathrm{A}}}\cdot l^2$.

Bewegung außerhalb des Kondensators

Im feldfreien Raum außerhalb des Kondensators wirken keine Kräfte und die Elektronen bewegen sich gleichförmig. Bis zum Auftreffen auf einem Schirm im Abstand $L$ vom Kondensator verstreicht die Zeit $t_L=\frac{L}{v_x}$. In dieser Zeit bewegt sich ein abgelenktes Elektron in $y$-Richtung um:

$y_L=v_l\cdot t_L=\sqrt{\frac{e}{2m_e{U}_{\mathrm{A}}}}\cdot \frac{U_C}{d}\cdot l\cdot \frac{L}{v_x}=\frac{U_C}{2d{U}_{\mathrm{A}}}\cdot l\cdot L$.

Insgesamt trifft der Strahl also mit folgendem Versatz auf dem Schirm auf:

$y_{\mathrm{g}\mathrm{e}\mathrm{s}}=y_l+y_L=\frac{U_{C}l}{2d{U}_{\mathrm{A}}}\cdot (\frac{l}{2}+L)$.

---

Aufgaben:

• Bahnkurvenberechnung in einer Braunschen Röhre.
  
• Energieerhaltung und Braunsche Röhre.

---

Ursache des elektrischen Feldes $\overrightarrow{E}$

Mit der Flächenladungsdichte: $\sigma :=\frac{q}{A},[\sigma ]=\frac{\mathrm{C}}{{\mathrm{m}}^{\mathrm{2}}}$ findet man:

Coulombsches Gesetz

Ladungen mit gleichem Vorzeichen stoßen sich ab, Ladungen mit unterschiedlichen Vorzeichen ziehen sich an. Wie hängt die Kraft vom Abstand der Kugeln ab?

Physik Oberstufe: Vorlage:Experiment-Box Wir wollen die Feldstärke im Abstand $r$ vom Kugelmittelpunkt berechnen. Da sich die Feldstärke $E$ durch vergrößern der Kugel nicht ändert, können wir der Kugel den Radius $r$ geben und die Feldstärke direkt über der Kugeloberfläche mit unserer Beziehung $\sigma ={\epsilon }_0\cdot E$ berechnen:

$\sigma =\frac{Q}{A}=\frac{Q}{4\pi r^2}={\epsilon }_0\cdot E⟹$

Coulomb-Kraft

Da $F_{\mathrm{e}\mathrm{l}}=q\cdot E$, gilt für die Kraft, die zwei Ladungen $Q_1$ und $Q_2$ im Abstand $r$ aufeinander ausüben, demnach das Coulombsche Gesetz: Physik Oberstufe: Vorlage:Hervorhebung

Coulomb-Potential

Wir interessieren uns für die potentielle Energie $W_{\mathrm{p}\mathrm{o}\mathrm{t}}$, die eine Ladung $q$ im Feld einer zweiten Ladung $Q$ besitzt. Dazu transportieren wir $q$ von $r_1$ nach $r_2$:

$W_{\mathrm{p}\mathrm{o}\mathrm{t}}=\underset{r_1}{\overset{r_2}{\int }}{F}_{\mathrm{e}\mathrm{l}}(r)\mathrm{d}\mathrm{r}=\underset{r_1}{\overset{r_2}{\int }}\frac{Q\cdot q}{4\pi {\epsilon }_0\cdot r^2}\mathrm{d}\mathrm{r}$

$=\frac{Q\cdot q}{4\pi {\epsilon }_0}{\left[\frac{-1}{r}\right]}_{r_1}^{r_2}=\frac{Q\cdot q}{4\pi {\epsilon }_0}(\frac{-1}{r_2}+\frac{1}{r_1}).$

Wenn wir $q$ nun in Gedanken bis ins Unendliche transportieren ($r_2\to \mathrm{\infty }$), so erhalten wir für die gesamte potentielle Energie der Ladung $q$, die diese im Abstand $r$ von $Q$ hat: Physik Oberstufe: Vorlage:Hervorhebung Im Unendlichen gilt: $W_{\mathrm{p}\mathrm{o}\mathrm{t}}=0$. Für das elektrische Potential $\phi :=\frac{\mathrm{\Delta }{W}_{\mathrm{p}\mathrm{o}\mathrm{t}}}{\mathrm{\Delta }q}$ im Abstand $r$ einer mit $Q$ geladenen Kugel gilt dann: Physik Oberstufe: Vorlage:Hervorhebung

---

Aufgabe: Superpositionsprinzip und Coulombsches Gesetz.

---

Der Kondensator als elektrisches Bauelement

Verschiedene Kondensatoren zur Montage auf Leiterplatten. Für Details anklicken.

Aus dem Experiment folgt die Proportionalität zwischen am Kondensator angelegter Spannung $U$ und gespeicherter Ladung $Q$: $Q\sim U⟹Q=C\cdot U$ mit der allein von der Bauart des Kondensators abhängigen Proportionalitätskonstanten $C$. Die Kapazität $C$ eines Kondensators ist definiert als:

$C:=\frac{Q}{U},[C]=\frac{\mathrm{C}}{\mathrm{V}}=\mathrm{F}(\text{Farad})$

Beim Plattenkondensator gilt:

$E=\frac{U}{d}$

$\sigma =\frac{Q}{A}={\epsilon }_0\cdot E⟹$

$Q=\frac{{\epsilon }_0\cdot A}{d}\cdot U$

---

Aufgaben:

• Veränderung des Plattenabstands eines geladenen Kondensators.
  
• Geladene Kondensatoren zusammenschalten.

---

Materie im elektrischen Feld

Kondensator mit Dielektrikum.

Wir berücksichtigen diesen Effekt durch die Dielektrizitätszahl ${\epsilon }_r$ und erhalten für die Kapazität des Plattenkondensators im allgemeinen Fall: Physik Oberstufe: Vorlage:Hervorhebung Die Werte für ${\epsilon }_r$ verschiedener Materialien finden sich in Tabellen.

Schaltungen von Kondensatoren

Parallelschaltung von Kondensatoren.

Reihenschaltung von Kondensatoren.

Parallelschaltung

Wir erhalten für die Parallelschaltung von zwei Kondensatoren:

$C_{\mathrm{r}\mathrm{e}\mathrm{s}}=C_1+C_2.$

Reihenschaltung

Wir erhalten für die Reihenschaltung von zwei Kondensatoren:

$C_{\mathrm{r}\mathrm{e}\mathrm{s}}=\frac{1}{\frac{1}{C_1}+\frac{1}{C_2}},$

$\frac{1}{C_{\mathrm{r}\mathrm{e}\mathrm{s}}}=\frac{1}{C_1}+\frac{1}{C_2}.$

---

Aufgaben:

• Reihen- und Parallelschaltung von Kondensatoren.
• Ein Kondensator, teilweise mit Dielektrikum gefüllt.

---

Energie elektrischer Felder

Frage: Wieviel Energie ist im Kondensator gespeichert? Physik Oberstufe: Vorlage:Experiment-Box

Diese Arbeit muss man von der ersten bis zur letzten Ladung aufsummieren (integrieren):

$W=\underset{0}{\overset{Q}{\int }}U(q)\cdot \mathrm{d}q=\underset{0}{\overset{Q}{\int }}\frac{q}{C}\cdot \mathrm{d}q=\frac{1}{C}\underset{0}{\overset{Q}{\int }}q\cdot \mathrm{d}q=\frac{1}{C}\cdot {\left[\frac{1}{2}{q}^2\right]}_0^Q.$

Man erhält damit dann: Physik Oberstufe: Vorlage:Hervorhebung

Wenn wir in $W=\frac{1}{2}C\cdot U^2$ für die Kapazität $C$ die Formel für den Plattenkondensator $C={\epsilon }_0{\epsilon }_r\frac{A}{d}$ und $U=d\cdot E$ einsetzen, so finden wir:

$W=\frac{1}{2}C\cdot U^2=\frac{1}{2}{\epsilon }_0{\epsilon }_{r}A\cdot d\cdot E^2=\frac{1}{2}{\epsilon }_0{\epsilon }_r\cdot E^2\cdot \underset{=V}{\underbrace{A\cdot d}}$

Die Energiedichte des elektrischen Feldes ist damit: Physik Oberstufe: Vorlage:Hervorhebung

Anziehungskraft zwischen Kondensatorplatten

Aus der im elektrischen Feld $\overrightarrow{E}$ des Kondensators gespeicherten Energie $W$ können wir die Anziehungskraft zwischen den Platten ableiten. Nach Abtrennen der Spannungsquelle ziehen wir die Platten um das Stückchen $\mathrm{\Delta }x$ auseinander. Dabei bleibt das Feld $\overrightarrow{E}$ konstant, wohingegen das Volumen um $\mathrm{\Delta }V=A\cdot \mathrm{\Delta }x$ zunimmt. Die allein von der Feldstärke $\overrightarrow{E}$ abhängende und damit ebenfalls konstante Energiedichte füllt das hinzugekommene Volumen $\mathrm{\Delta }V$ mit der zusätzlichen Energie, die beim Auseinanderziehen gegen die Anziehungskraft der Platten aufgebracht werden muss:

$\mathrm{\Delta }W=F\cdot \mathrm{\Delta }x=\underset{=F}{\underbrace{\frac{1}{2}{\epsilon }_0{\epsilon }_r\cdot E^2\cdot A}}\cdot \mathrm{\Delta }x$

Für die Anziehungskraft zwischen Kondensatorplatten erhält man also: Physik Oberstufe: Vorlage:Hervorhebung

Auf- und Entladung eines Kondensators

Spannungsverlauf bei der Auf- und Entladung eines Kondensators.

Im Folgenden bestimmen wir den zeitlichen Verlauf der Ladung $Q(t)$ beim Auf- und Entladen eines Kondensators $C$ über einen Widerstand $R$. Durch Anwendung der Maschenregel erhält man:

$U_0=U_R+U_C=R\cdot I(t)+\frac{Q(t)}{C}.$

Mit $I(t)=\dot{Q}(t)$ ergibt sich eine Differentialgleichung (DGL) für $Q(t)$:

$\dot{Q}(t)=\frac{U_0}{R}-\frac{Q(t)}{RC}.$

Gesucht ist die Funktion $Q(t)$, die diese Differentialgleichung erfüllt. Außerdem muss im Moment des Einschaltens $t=0$ die jeweilige Anfangsbedingung erfüllt sein.

Kennen wir $Q(t)$, so können wir alle anderen elektrischen Größen leicht berechnen:

$U_C(t)=\frac{Q(t)}{C},I(t)=\dot{Q}(t).$

Aufladung

Wird der entladene Kondensator durch schließen des Schalters aufgeladen, so gilt die Anfangsbedingung:

$U_C(0)=\frac{Q(0)}{C}=0.$

Die Lösung der DGL lautet in diesem Fall: Physik Oberstufe: Vorlage:Hervorhebung

Entladung

Wird der geladenen Kondensator über der Widerstand $R$ entladen, so entfällt die Spannungsquelle und die DGL wird zu:

$\dot{Q}(t)=-\frac{1}{RC}Q(t).$

Außerdem gilt die Anfangsbedingung:

$U_C(0)=\frac{Q(0)}{C}=U_0.$

Die Lösung der DGL lautet in diesem Fall: Physik Oberstufe: Vorlage:Hervorhebung

---

Aufgaben:

• Lösung der Differentialgleichung.
• Herleitung der im Kondensator gespeicherten Energie.

---

Bestimmung der Ladung eines Elektrons

Öltröpfchenversuch nach Millikan

Prinzipskizze

Mit dem Millikan-Versuch kann die Ladung eines Elektrons (Elementarladung) gemessen werden. Dazu beobachtet man geladene Öltröpfchen, die sich unter Einfluss der Gravitationskraft und der elektrischen Kraft im vertikalen elektrischen Feld eines Plattenkondensators bewegen. Aus Steig- und Fallgeschwindigkeit sowie der jeweils anliegenden Spannung am Kondensator lässt sich die Elementarladung bestimmen.

Schwebemethode

Bei dieser Methode geht man folgendermaßen vor:

• man ermittelt die Spannung, bei der ein Öltröpfchen schwebt,
• man misst die Geschwindigkeit, mit der das Öltröpfchen bei abgeschalteter Spannung sinkt.

Auswertung

Datei:Millikan experiment.ogv Für das schwebende Öltröpfchen gilt:

$F_{\mathrm{e}\mathrm{l}}=F_{\mathrm{G}}⟹q\cdot E=m\cdot g$

$⟹q\cdot \frac{U}{d}=\frac{4}{3}\pi r^3\cdot {\rho }^{\prime }\cdot g$

$⟹q=\frac{4\pi r^3\cdot {\rho }^{\prime }g\cdot d}{3U}$

Dabei ist ${\rho }^{\prime }$ die effektive Dichte, die die Auftriebskraft der Tröpfchen in Luft mit einbezieht. Bei Kenntnis des Radius $r$ könnten wir $q$ direkt berechen. Die Öltröpfen sind zur direkten Messung von $r$ jedoch viel zu klein.

Stattdessen bestimmen wir $r$ aus der Sinkgeschwindigkeit. Im freien Fall des Öltröpfchens stellt sich ein Kräftegleichgewicht aus Gewichtskraft und Luftreibungskraft $F_{\mathrm{R}}$ (Stokessche Reibung) ein:

$F_{\mathrm{R}}=F_{\mathrm{G}}⟹6\pi \eta r\cdot v=\frac{4}{3}\pi r^3\cdot {\rho }^{\prime }\cdot g$

$⟹r=\sqrt{\frac{9\eta \cdot v}{2{\rho }^{\prime }g}}$

Dabei ist $\eta$ die Viskosität der Luft. Eingesetzt in die Formel für $q$ findet man: Physik Oberstufe: Vorlage:Hervorhebung Diese Formel hängt nur noch von bekannten Konstanten und den gemessenen Größen Spannung und Fallgeschwindigkeit ab.

Gleichfeldmethode

Steigen im Feld

Sinken im Feld. (Die Beträge der Vektoren sind im Vergleich mit dem Steigen nicht korrekt dargestellt.)

Eine Schwierigkeit der Schwebemethode ist, den Schwebezustand (v=0) und damit die zugehörige Spannung genau zu bestimmen. Die Öltröpfchen driften meist hin und her und müssen durch Änderung der Spannung wieder „zurückgeholt“ werden.

Darum liefert die in diesem Abschnitt beschriebene Gleichfeldmethode meist bessere Resultate. Man geht folgendermaßen vor:

• bei fest vorgegebener Spannung bestimmt man die Geschwindigkeit, mit der das Öltröpfchen steigt,
• anschließend polt man den Kondensator um und misst die Geschwindigkeit, mit der das Öltröpfchen nun sinkt.

Auswertung

Im Falle des Steigens mit $v_2$ gilt:

$F_{\mathrm{e}\mathrm{l}}=F_{\mathrm{G}}+F_{\mathrm{R}}⟹q\cdot E=m\cdot g+6\pi \eta r\cdot v_2$.

Im Falle des Sinkens mit $v_1$ gilt entsprechend:

$F_{\mathrm{e}\mathrm{l}}+F_{\mathrm{G}}=F_{\mathrm{R}}⟹q\cdot E+m\cdot g=6\pi \eta r\cdot v_1$.

Wir addieren diese Gleichungen, setzen $E=\frac{U}{d}$ und erhalten damit:

$q\cdot \frac{U}{d}=3\pi \eta r\cdot (v_1+v_2)⟹q=\frac{3d\pi \eta r}{U}\cdot (v_1+v_2)$.

Subtrahieren wir stattdessen die Gleichungen und setzen wir wieder $m=\frac{4}{3}\pi r^3\cdot {\rho }^{\prime }$, so erhalten wir:

$m\cdot g=3\pi \eta r\cdot (v_1-v_2)⟹\frac{4}{3}\pi r^3\cdot {\rho }^{\prime }\cdot g=3\pi \eta r\cdot (v_1-v_2)$.

Auflösen nach $r$ ergibt:

$⟹r=\frac{3}{2}\sqrt{\frac{\eta }{{\rho }^{\prime }g}\cdot (v_1-v_2)}$.

Diese Beziehung für $r$ setzen wir jetzt in die Formel für $q$ ein: Physik Oberstufe: Vorlage:Hervorhebung Aus den gemessenen Größen Spannung, Steig- und Sinkgeschwindigkeit können wir $q$ bestimmen.

Ergebnis und Bemerkungen

Messergebnisse für die Ladung der Tröpfchen beim Millikan-Versuch. Es treten nur Vielfache der Elementarladung $e$ auf.

Wiederholt man die Messung der Ladung für viele verschiedene Öltröpfchen, so findet man unterschiedliche Ladungen $q$. In der Tat werden die Öltröpfchen unterschiedlich viele zusätzliche Elektronen tragen bzw. eine unterschiedlich große Anzahl von Elektronen wird dem Tröpfchen jeweils fehlen. Bei genauer Untersuchung findet man aber, dass alle Öltröpfchen ganzzahlige Vielfache einer Elementarladung:

$e=1.602\cdots \times 10^{-19}\mathrm{C}$

tragen. Dieser kleinste gemeinsame Teiler der unterschiedlichen Ladungen ist der Betrag der Ladung des Elektrons.

---

Man kann das Experiment und auch die Auswertung weiter verbessern. Hinweise dazu finden sich u.a. auf LEIFI, wo das Experiment auch simuliert werden kann, und in der Link-Sammlung des zugehörigen Wikipedia Artikels. Beachtenswert ist auch der englische Wikipedia Artikel und die dortige Ausführung zur historischen Entwicklung.