Mathe für Nicht-Freaks: Komplexe Zahlen: Darstellung komplexwertiger Funktionen
{{#invoke:Mathe für Nicht-Freaks/Seite|oben}}
Motivation
Wenn wir eine Funktion untersuchen wollen, ist es hilfreich, sich einen Funktionsgraphen aufzuzeichnen. Betrachten wir beispielsweise die Funktion .

Die -Achse ist ein Zahlenstrahl. Mit dem Zahlenstrahl kann man reelle Zahlen darstellen, indem man sie als Punkte auf diesem Zahlenstrahl markiert, zum Beispiel so:

Das Bild dieser drei Punkte unter der Funktion kann man auf einem anderen Zahlenstrahl darstellen.

So ist aber noch nicht klar, zu welchem Eingabewert welcher Funktionswert gehört. Es könnte beispielsweise auch und gelten. Also sollten wir die Punkte beschriften. Das sieht dann so aus:

Wenn wir sehr viele Punkte betrachten, kann diese Methode schnell unübersichtlich werden. Daher verwendet man meistens einen Funktionsgraphen um den Zusammenhang zwischen den beiden Werten zu veranschaulichen.

Hierbei stellt man die zwei Geraden senkrecht zueinader und nutzt zur Visualisierung die gesamte zwischen ihnen aufgespannte Fläche. Das braucht zwar mehr Platz, aber der eingezeichnete Funktionsgraph ermöglicht eine sehr übersichtliche Zuordnung von Eingabewerten zu den zugehörigen Funktionswerten. Wir können diese Funktion also mit zwei 1D-Plots (Zahlenstrahl) oder mit einem 2D-Plot (Koordinatensystem) darstellen.
In den letzten Kapiteln haben wir die komplexen Zahlen kennengelernt. Wir haben Funktionen von nach betrachtet, wie . Wie können wir eine solche Funktion darstellen?
Eine gute Möglichkeit, komplexe Zahlen zu visualisieren, ist die Gaußsche Zahlenebene. Hierbei identifiziert man jede komplexe Zahl mit dem Punkt im . Statt einem eindimensionalen Zahlenstrahl verwendet man eine zweidimensionale Zahlenebene. Nun wollen wir aber jeweils die Eingabewerte und die zugehörigen Funktionswerte gleichzeitig darstellen. Im Reellen braucht man dafür zwei 1D-Plots (Zahlenstrahl) oder einen dimensionalen Graphen (Koordinatensystem). Analog braucht man im Komplexen zwei 2D-Plots (Zahlenebene) oder einen dimensionalen Graphen. Wie soll ein 4D-Plot aussehen?
Darstellung von Funktionen
Wir überlegen uns zunächst, wie wir eine Funktion darstellen können. Eine solche Funktion ordnet jeder reellen Zahl auf der Zahlengeraden eine komplexe Zahl in der Gaußschen Zahlenebene zu. Wir werden zwei Möglichkeiten vorstellen, wie man sich davon ein Bild machen kann. Da die Definitionsmenge von eindimensional und die Wertemenge von zweidimensional ist, benötigen wir nach unseren vorherigen Überlegungen einen -dimensionalen Funktionsgraphen zur Darstellung von . Wir müssen also zu den zwei Dimensionen unseres Papiers eine weitere hinzufügen. Dafür können wir entweder von der Ebene in den Raum übergehen oder aber die Zeit als dritte Dimension verwenden.
Darstellung in der komplexen Ebene mit Zeit als Eingabeparameter
Wir stellen uns den reellen Eingabeparameter unserer Funktion als Zeit vor. Jedem Zeitpunkt ist also eine komplexe Zahl zugeordnet. Diese komplexe Zahl zeichnen wir als Punkt in ein zweidimensionales Koordinatensystem ein. Der Graph der Funktion beschreibt also, wie sich ein Punkt innerhalb der Ebene im Laufe der Zeit bewegt:

Wir haben auch den Weg mit eingezeichnet, den unser Punkt zurücklegt. Das sind alle komplexe Zahlen, die als Funktionswert von vorkommen, also das Bild von . Der Weg alleine würde allerdings nicht ausreichen, um die Funktion zu beschreiben. Es wäre nämlich nicht klar, in welcher Richtung, wie schnell oder wie oft dieser Weg durchlaufen wird. Daher müssen wir angeben, welche reellen Eingabeparameter zu welchen der dargestellten Funktionswerten gehören. Diese Zuordnung geschieht erst durch die Bewegung des markierten Punktes im Laufe der Zeit. Vorlage:Todo
Beispiele
3D-Darstellung als Punkte im Raum
Um eine Graphik von zu erhalten, die sich nicht bewegt, bringen wir einfach die dritte Raumdimension ins Spiel. Wir zeichnen also alle Punkte der Form mit in ein dreidimensionales Koordinatensystem ein. Sofern unsere Funktion stetig ist, erhalten wir dadurch eine Kurve im dreidimensionalen Raum. Vorlage:Todo Schneiden wir diese Kurve für ein gewisses mit der Ebene (diese Ebene verläuft parallel zur --Ebene), so erhalten wir genau den Punkt , der bei der vorherigen Darstellung zum Zeitpunkt erscheint. Wir können also aus unserer 3D-Darstellung wieder die Bewegung eines Punktes innerhalb der Ebene zurückerhalten, indem wir die --Ebene mit gleichbleibender Geschwindigkeit von links nach rechts wandern lassen. Vorlage:Todo Wenn wir die Projektion der Kurve auf die --Ebene betrachten, so erkennen wir den gewöhnlichen 2D-Graphen der reellwertigen Funktion . Und bei Projektion auf die - Ebene erhält man den Graphen der reellwertigen Funktion . Vorlage:Todo
Darstellung von Funktionen
In diesem Abschnitt wollen wir Funktionen der Form grafisch darstellen. Jeder Zahl in der komplexen Zahlenebene wird von der Funktion eine reelle Zahl zugeordnet. Eine Möglichkeit wäre, an jedem Punkt in der komplexen Zahlenebene eine Beschriftung mit dem zugehörigen Funktionswert anzubringen. Betrachtet man nur endlich viele von diesen Beschriftungen (damit man das noch lesen kann), sieht das beispielsweise so aus:
In diesem Fall funktioniert das noch ganz gut, aber bei komplizierteren Funktionen ist klar, dass das Bild nicht mehr so leicht zu überblicken ist. Daher werden wir diese Idee ein wenig modifizieren.
3D-Darstellung einer Fläche über der komplexen Ebene
Anstatt bei jedem Punkt der komplexen Ebene eine Beschriftung anzubringen, auf der der Funktionswert steht, können wir die dritte Dimension zur Hilfe nehmen. Wir zeichnen über der komplexen Zahl in der Gaußschen Zahlenebene einen Punkt in der Höhe von ein. Es entsteht eine Fläche.
2D-Darstellung mit Höhenlinien auf der komplexen Ebene
Wenn wir die Grafik nicht mit dem Computer, sondern per Hand erstellen wollen, bietet sich die Darstellung als 3D-Plot nicht an. Man betrachtet wieder die komplexe Zahlenebene. In diesem Fall wollen wir auch den Funktionswert eines Punktes an diesem Punkt darstellen.
Eine Möglichkeit sind Höhenlinien. Wir stellen hierbei nicht an jedem Punkt aus der komplexen Zahlenebene seinen Funktionswert dar, sondern nur an manchen. Diese komplexen Zahlen wählen wir folgendermaßen aus: Es sollen nur mit dargestellt werden. Jede dieser Zahlen markieren wir durch eine blaue Färbung.
Für die Funktion ergibt sich folgendes Bild.

Ein Problem hierbei ist, dass wir nicht wissen, auf welche Funktionswerte die blau markierten Zahlen genau abgebildet werden. Wir wissen nur, dass diese Werte natürliche Zahlen sind. Wie können wir mit diesem Bild zeigen, welche komplexen Zahlen auf abgebildet werden? Wir markieren diese Zahlen einfach rot und nicht blau.

Wir erhalten eine Linie. Das ist sehr praktisch, denn jetzt müssen wir nicht mehr jede Zahl, die wir blau markiert haben, einzeln beschriften, sondern wir beschriften einfach Linien.

Beispiele
Darstellung von Funktionen
2D-Darstellung mit Farben und Helligkeit
Erklärung
Wir wollen untersuchen, wie wir Funktionen von den komplexen Zahlen in die komplexen Zahlen anschaulich darstellen können. Das heißt, wir betrachten eine Funktion . Komplexe Zahlen lassen sich in der Gaußschen Zahlenebene darstellen. Folglich benutzen wir zum Abbilden einer komplexen Zahl zwei Dimensionen. Um nun den Graphen von anzugeben, brauchen wir also einen 4D-Plot. Wir haben aber auf einem Papier nur zwei und in unserer Welt nur drei Dimensionen zur Verfügung. Es gibt aber andere Möglichkeiten, die Funktion anschaulich wiederzugeben.
Im Folgenden werden wir verschiedene Arten kennenlernen, wie man solche Graphen visualisieren kann.
Es gibt mehrere Varianten eine komplexe Zahl darzustellen. Einmal in kartesischen Koordinaten mittels Real- und Imaginärteil: , mit . Und andererseits mit Polarkoordinaten: , wobei und . Meistens nutzen wir zur Veranschaulichung Real- und Imaginärteil, nun können wir die Polarkoordinaten verwenden. Aber wie lässt sich der Betrag und der Winkel darstellen? Wir können zum Beispiel, den Winkel mit einer Farbe und den Betrag mit der Helligkeit oder der Sättigung zu identifizieren. Der Winkel soll -periodisch sein. Also ist es sinnvoll, die verschiedenen Winkel auf einen Farbkreis abzubilden. Den Betrag als Farbsättigung aufzufassen, macht auch Sinn. Denn für den Betrag gibt es eine untere Grenze, nämlich die Null. Genauso gibt es für die Helligkeit eine untere Grenze, nämlich volle Sättigung, also schwarz. Außerdem wird der Zahl kein Winkel zugeordnet und so hat auch Schwarz keine Farbe.
In diesem Bild wird diese Zuordnung veranschaulicht. Jede komplexen Zahl in der Gaußschen Ebene wird in ihrer Farbe und Sättigung abgebildet.
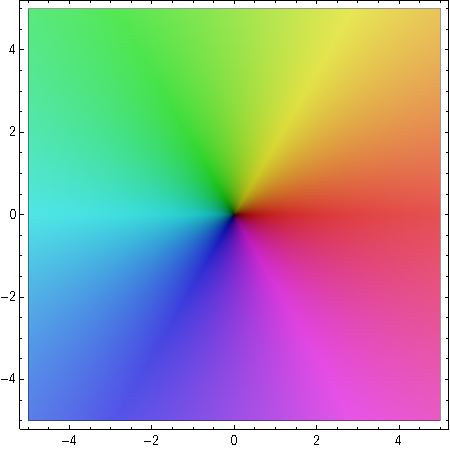
Je größer der Betrag einer Zahl ist, desto heller ist der Punkt. Die Farben verlaufen in -Schritten von Rot über Gelb, Grün, dann Cyan und Blau zu Magenta. Also beschreiben zum Beispiel Rot und Cyan die reelle Achse.
Nun kennen wir also eine Art komplexe Zahlen mittels Farben und Sättigung darzustellen. Wie hilft uns das nun beim Plotten von komplexen Funktionen? Da wir nun zwei verschiedene Möglichkeiten haben komplexe Zahlen zu veranschaulichen, können wir diese jeweils auf den Definitions- und den Bildbereich anwenden. Wir stellen nun eine komplexe Zahl mittels Real- und Imaginärteil dar wobei . Dann können wir das Bild in Polarkoordinaten betrachten .
Das heißt, wir suchen uns einen Punkt in der Gaußschen Zahlenebene. Nun bilden wir diesen mit ab. Das Ergebnis ist eine komplexe Zahl mit einem bestimmten Winkel und Betrag, die wir mit Farbe und Sättigung veranschaulichen können. Dem Punkt wird also die Farbe und Sättigung des Punktes zugeordnet.
Machen wir dies nun mit jedem Punkt in erhalten wir einen Graphen der komplexen Funktion .
Einfache Beispiele
Rationale Funktionen
Im Folgenden untersuchen wir kompliziertere Polynome und gebrochen rationale Funktionen. Bei solchen Funktionen interessieren uns besonders die Nullstellen und die Polstellen. Da die Null in unserer Darstellung schwarz ist, können wir leicht die Nullstellen als schwarze Punkte ausmachen. Für Polstellen divergiert der Betrag der Funktion gegen Unendlich, also können wir diese Punkte mit Weiß darstellen.
Betrachten wir beispielsweise die Funktion , so ist diese bei nicht definiert, da kein sinnvoller Funktionswert zugeordnet werden kann. Allgemein definieren wir gebrochen-rationale Funktionen nur auf . Somit dürfen wir bei den Polstellen die komplexe Ebene nicht in einer bestimmten Art und Weise einfärben. Das macht im Bild keinen Unterschied, da wir einen einzelnen Punkt der komplexen Ebene in unserer Grafik nicht wahrnehmen können. Dass die Grafik bei einer Polstelle weiß erscheint ist richtig, da komplexe Zahlen in der Nähe dieser Polstellen auf komplexe Zahlen mit sehr großen Beträgen abgebildet werden. Vorlage:Todo
| Bild | Beschreibung |
|---|---|
 |
Dieses Polynom ist bereits faktorisiert. Die schwarzen Punkte in der Grafik sind jeweils bei den Nullstellen. |
 |
Hier ist der Funktionsterm noch nicht faktorisiert. Um also die Nullstellen abzulesen, müssen wir ihn zuerst umformen. Wir kennen die reelle Nullstelle des Polynoms , uns fehlen noch zwei komplexe. Durch Polynomdivision kann man berechnen: . Nun können wir mit der Lösungsformel die beiden anderen Nullstellen herausfinden: . Somit gilt . Ein Polynom dritten Grades hat im komplexen also genau drei Nullstellen. Außerdem sehen wir, dass das Bild unter einer Drehung um bzw. gleich bleibt. Um dies zu untersuchen, benutzen wir Polarkoordinaten . Es gilt nämlich . |
 |
Dieses gebrochen-rationale Funktion ist bereits faktorisiert. Die schwarzen Punkte in der Grafik sind jeweils bei den Nullstellen, die weißen Punkte sind bei den Polstellen. |
 |
Wir faktorisieren den Funktionsterm: Vorlage:Einrücken Nun können wir die Polstellen und Nullstellen einfach ablesen. Betrachten wir in dem Bild nur die reelle Achse, sehen wir, dass sie nur cyan und rot eingefärbt ist. Cyan steht für die negativen reellen Zahlen und rot für die positiven. Das heißt (wenn man die Polstelle ignoriert). Was Sinn ergibt, da die Funktionsvorschrift nur reelle Zahlen beinhaltet. |
 |
Zunächst faktorisieren wir die Funktionsvorschrift: Vorlage:Einrücken Anhand des faktorisierten Funktionsterms kann man leicht die Lage der Null- und Polstellen bestimmen. Es fällt auf, dass die Grafik bei betragsmäßig großen Zahlen ungefähr grün eingefärbt ist. Das kann man durch folgende Rechnung erklären: Vorlage:Einrücken Der komplexen Zahl wird die Farbe grün zugeordnet. |
 |
Hier sehen wir ein Beispiel einer gebrochen rationalen Funktion mit doppelter Nullstelle und dreifacher Polstelle. Die doppelte Nullstelle hat eine viel dunklere Umgebung als die einfache Nullstelle. In dieser Darstellung können wir die Vielfachheit der Null- und Polstellen sogar ablesen. Die einfache Nullstelle bei wird von jeder Farbe einmal umgeben, wobei die Doppelte Nullstelle von jeder Farbe zweimal umgeben ist. Und die dreifache Polstelle bei wird von jeder Farbe dreimal berührt. |
 |
In diesem Bild ist eine Funktion mit sieben Polstellen abgebildet. Eine davon liegt im Ursprung und der Rest ist regelmäßig auf dem Einheitskreis verteilt. Denn es gilt . Es ist schnell zu sehen, dass eine Polstelle im Punkt liegt. Aber wieso folgt daraus, dass sechs Nullstellen auf dem Einheitskreis liegen? Um das zu untersuchen, bietet sich die Polardarstellung der komplexen Zahlen an. Wir fragen uns, wann gilt : Vorlage:Einrücken Daraus folgt , da . Also muss gelten für ein . Diese Gleichung wird von für alle erfüllt. Also liegen die Polstellen bei für (wir benutzen hier nur diese Eingaben für , da sich die Werte wiederholen). Was wir noch betrachten können ist das Verhalten der Funktion im Unendlichen: Vorlage:Einrücken Daher wird es nach außen immer dunkler. |
Kompliziertere Beispiele
| Bild | Beschreibung |
|---|---|
 |
Auf diesem Bild ist die Exponentialfunktion dargestellt. Wir erinnern uns, dass wir für die Farbkodierung von die Polardarstellung verwendet haben. Die Polardarstellung hängt also eng mit der Exponentialfunktion zusammen. In diesem Fall ist selbst die Exponentialfunktion. Somit gilt , sodass wir die Polardarstellung direkt am Real- und Imaginärteil von ablesen können. Der Realteil von beschreibt also die Helligkeit und der Imaginärteil von die Farbe des Bildpunktes. Da die reelle Exponentialfunktion streng monoton steigend ist, wird das Bild von links nach rechts immer heller. Wenn wir uns hingegen parallel zur imaginären Achse bewegen, bleibt die Helligkeit konstant und der Farbton ändert sich gleichmäßig, sodass sich ein Regenbogenmuster bildet. Hieran sieht man auch deutlich die -Periodizität der Exponentialfunktion. |
 |
Hier sehen wir die Sinusfunktion. Wir wissen bereits, dass auch in den komplexen Zahlen die einzigen Nullstellen des Sinus bei für liegen. Dies erklärt die schwarzen Punkte, die im Abstand von auf der reellen Achse auftauchen. Außerdem sehen wir, dass der Sinus eine -periodische Funktion ist, und zwar nicht nur für reelle Argumente. Wenn wir nochmals die reelle Achse betrachten, erkennen wir, dass die Intervalle zwischen den Nullstellen abwechselnd rot und cyan sind. Denn dort sind die Funktionswerte bekanntermaßen reell und sind abwechselnd positiv und negativ zwischen den Nullstellen. Eine positive reelle Zahl hat den Winkel und erscheint somit rot, eine negative reelle Zahl hat den Winkel und erscheint somit cyan. Wenn wir weiter weg von der reellen Achse gehen, nähert sich das Bild einem Regenbogenmuster mit vertikal verlaufenden Linien des gleichen Farbtons an, die nach außen, also für betragsmäßig große Imaginärteile, immer heller werden. Dies können wir mithilfe der Definition des Sinus über die Exponentialfunktion erklären. Es gilt Vorlage:Einrücken Für einen großen positiven Imaginärteil gilt und folglich Vorlage:Einrücken Der Betrag ist also ungefähr und nimmt mit wachsendem Imaginärteil immer weiter zu. Das Bild wird also nach oben immer heller. Der Winkel beträgt in etwa und hängt daher für große Imaginärteile fast linear vom Realteil ab (und ist nahezu unabhängig vom Imaginärteil). Deshalb wird ein vertikales Regenbogenmuster sichtbar. Für einen sehr negativen Imaginärteil können wir hingegen abschätzen. In analoger Weise zu obiger Rechnung ergibt sich daraus schließlich Vorlage:Einrücken In der unteren Halbebene zeigt sich also das gleiche Phänomen wie in der oberen Halbebene, nur ist die Richtung des Farbverlaufs andersherum. |
 |
Wir haben uns bereits überlegt, dass gilt. Das Bild der Kosinusfunktion entsteht also aus dem vorangegangenen Bild der Sinusfunktion durch eine Verschiebung um nach links. Folglich übertragen sich alle Phänomene (Nullstellen, Regenbogenmuster usw.) auf die Darstellung der Kosinusfunktion. |
 |
Hier sehen wir die Tangensfunktion . Die Nullstellen sind die Nullstellen des Sinus und die Polstellen sind die Nullstellen des Kosinus. Daher befinden sich für an den Stellen schwarze und an den Stellen weiße Punkte. Das Verhalten der reellen Tangensfunktion kennen wir: Auf dem Intervall von einer Nullstelle zur nächsten Polstelle ist sie positiv und auf dem Intervall von einer Polstelle zur nächsten Nullstelle ist sie negativ. Dies erklärt die Bereiche in rot und cyan auf der reellen Achse. Wie verhält sich der Tangens aber für Imaginärteile in hinreichend großem Abstand zur ? Für großes verwenden wir wieder die Annäherung Vorlage:Einrücken Für die um nach links verschobene Kosinusfunktion ergibt sich entsprechend Vorlage:Einrücken Somit ist Vorlage:Einrücken Der Tangens ist also nahezu konstant! Dies begründet, warum die obere Halbebene fast vollständig die gleiche Farbe trägt. Sie ist grün, denn dies ist die Farbkodierung von . Auf der unteren Halbebene können wir eine ähnliche Approximation benützen, die zu führt. Alternativ können wir verwenden, um für sehr negative zu erhalten. Die Farbkodierung von ist lila. Also erscheint die untere Halbebene fast komplett in lila. |
 |
Die Funktion ist genauso wie die Funktion an der Stelle nicht definiert. Im Gegensatz zu der rationalen Funktion handelt es sich hier jedoch bei dem Nullpunkt nicht um eine gewöhnliche Polstelle. Auf dem Bild sieht unsere Funktion um die herum auch ziemlich merkwürdig aus. Wir wollen versuchen, einige Beobachtungen zu erklären. Betrachten wir zunächst auf den reellen Zahlen. Für gilt und folglich . Dies erklärt, warum das Bild auf der reellen Achse nach links und rechts langsam rot wird. Für mit gilt und somit . Für mit gilt und somit . Wenn wir uns der also von rechts nähern, wird das Bild fast weiß. Und wenn wir uns von links nähern, wird es fast schwarz. Doch was passiert, wenn wir uns aus anderen Richtungen der nähern? Wir untersuchen exemplarisch den Fall mit und . Wir nähern uns der also von oben. Es gilt Vorlage:Einrücken Die Funktionswerte haben auf der positiven imaginären Achse demnach alle den Betrag (also konstante Helligkeit) und verändern ihren Winkel gemäß der Funktion . Für welche wird ein bestimmter Winkel, zum Beispiel (also der Farbton rot), angenommen? Genau dann, wenn es ein mit gibt, das heißt an den Stellen für . Damit gilt, wählen wir . Wir sehen, dass das Bild für an unendlich vielen Stellen rot eingefärbt ist, und diese Stellen haben bei einen Häufungspunkt. Das gleiche gilt aber auch für alle anderen Farben, nicht nur für rot. Nähern wir uns der von oben, wechseln sich die Farben also immer schneller und schneller ab. Insofern ist es naheliegend, den Punkt in diesem Bild einfach als bunt zu bezeichnen. |
 |
Die Funktion ist wieder bei nicht definiert. Auf der reellen Achse nimmt auch nur reelle Werte an. Außerdem gilt, für läuft von oben gegen . Da für gilt, ist das Bild auf der rechten Seite rot. Links wird die Abbildung cyan. Denn für läuft von unten gegen und für gilt . Außerdem folgt aus , dass und damit . Deshalb wird der Graph nach außen hin immer dunkler. Weil der Sinus nur reelle Nullstellen hat, gilt dies auch für . Die Nullstellen des Sinus liegen bei für . Also hat unsere Funktion Nullstellen genau bei für alle . Für gilt . Die Nullstellen haben somit einen Häufungspunkt bei . Wie wir auf dem Bild auch sehen kommen die schwarzen Punkte, also die Nullstellen, unendlich nah an die Null heran. Bei der Darstellung des Sinus kann man sehen, dass jede Nullstelle mit allen Farben umgeben ist. Das Gleiche folgt dementsprechend auch für . Wie wir aber schon wissen haben die Nullstellen einen Häufungspunkt in . Folglich haben alle Farben einen Häufungspunkt in der . Wieder kann man den Punkt bunt nennen. |
Darstellung von Bildern einzelner Punkte oder Gitterlinien
Um eine Funktion zu visualisieren, können wir zwei Gaußsche Zahlenebenen betrachten. Eine für den Eingabeparameter und eine für das Bild der Funktion. Wir können einen Eingabeparameter in der ersten Ebene markieren und in der zweiten Ebene sein Bild einzeichnen.
Anstatt nur einen Punkt zu betrachten, können wir auch das Bild einer Gerade betrachten.
Wir können auch ein Rechteck mit Gitterlinien betrachten.
Wir können das Rechteck auch einfärben, damit man weiß, welcher Punkt wohin abgebildet wird.
Darstellung von Real- und Imaginärteil des Bildes als Funktion
Wenn wir uns bei einer Funktion nur für den Real- oder den Imaginärteil interessieren, reicht es, die Funktionen und zu visualisieren. Dafür können wir die Methoden benutzen, die wir im Abschnitt zur Darstellung von Funktionen eingeführt haben. Wir können Real- und Imaginärteil also entweder dreidimensional als Fläche oder zweidimensional über Höhenlinien darstellen.
3D-Darstellung als Fläche
Bei der 3D-Darstellung können wir die Fläche zusätzlich mithilfe unserer Farbkodierung komplexer Zahlen mit dem Funktionswert einfärben. Wenn wir auf die Fläche von oben schauen würden, würden wir also unsere farbkodierten 2D-Grafiken erkennen. Hier sehen wir den Real- und Imaginärteil der Funktion nebeneinander:
-
Realteil
-
Imaginärteil
2D-Darstellung mit Höhenlinien
Betrachtung des -Teils
In den Beispielen im nächsten Abschnitt werden wir jedoch den Real- und Imaginärteil nicht als zwei getrennte Bilder zeigen. Stattdessen lassen wir die Darstellungen von Real- und Imaginärteil in einer Animation fließend ineinander übergehen. Das geht so: Den Imaginärteil einer komplexen Zahl können wir auch als den Realteil der um im Uhrzeigersinn gedrehten Zahl auffassen. Es gilt also . Wenn wir nun für betrachten, so sehen wir für den Real- und für den Imaginärteil von . Um keinen Sprung in der Animation zu haben, vollziehen wir eine vollständige Drehung und lassen von bis wandern. Wir sehen also nacheinander den Realteil, den Imaginärteil, den negativen Realteil und den negativen Imaginärteil.
Beispiele
| 3D-Bild | 2D-Bild | Beschreibung |
|---|---|---|
 |
 |
Wenn wir den -Teil der Identität betrachten, sehen wir eine Ebene durch den Ursprung, die in Richtung die Steigung und in die dazu senkrechte Richtung die Steigung besitzt. Die Höhenlinien verlaufen stets entlang der Richtung mit Steigung . Beim Realteil sind sie somit horizontal und beim Imaginärteil vertikal. |
 |
 |
Betrachten wir den Realteil der Funktion , so erkennen wir eine Sattelfläche, die von zwei Parabeln aufgespannt wird. Die nach oben geöffnete Parabel befindet sich über der reellen Achse und die nach unten geöffnete Parabel über der imaginären Achse. Dies liegt daran, dass für reelle Zahlen gilt, dass sowie . Soeben haben wir den -Teil für betrachtet. Nun erhöhen wir mit konstanter Geschwindigkeit und betrachten die Darstellung der reellwertigen Funktion . Es gilt Vorlage:Einrücken Der -Teil entspricht also dem Realteil an der um im Uhrzeigersinn gedrehten Stelle. Daher dreht sich unsere Grafik mit halber Geschwindigkeit gegen den Uhrzeigersinn. Insbesondere erhalten wir bei dem Imaginärteil () eine um gedrehte Darstellung im Vergleich zum Realteil. Bei der Darstellung der Höhenlinien wird dies noch deutlicher. Die beiden aufeinander senkrecht stehenden Geraden gehören zur Höhe , dies sind also genau die Nullstellen von Real- bzw. Imaginärteil. |
 |
 |
Wir erkennen, dass die dargestellte Fläche drei Senkungen und drei Hebungen aufweist. Es handelt sich wieder um eine Art Sattel, aber dieses Mal um einen Affensattel, da zusätzlich zu den beiden Ausbuchtungen für die Beine des Reiters eine dritte Ausbuchtung benötigt wird. Warum dieses Phänomen auftritt, wollen wir zunächst wieder am Realteil erklären und überlegen uns dann anschließend, warum der -Teil nur eine gedrehte Version davon ist. Bei der Betrachtung von bietet es sich an, die Polardarstellung zu verwenden. Es gilt . Bis auf den Faktor entspricht der Realteil von also dem Realteil von . Dieser wird maximal für mit und minimal für mit . Wir können stets so wählen, dass gilt. Folglich ist und damit , womit wir die drei Maxima des Realteils bei und die drei Minima bei erhalten. Dies erklärt die drei Hebungen und Senkungen, die mit einer -Symmetrie um den Ursprung angeordnet sind. Tatsächlich weist sogar die gesamte Funktion eine Drehsymmetrie um auf, wie aus der Rechnung Vorlage:Einrücken hervorgeht. Bei der Untersuchung des -Teils stellt sich ähnlich wie bei der Quadratfunktion heraus, dass Vorlage:Einrücken gilt. Daher dreht sich unsere Grafik mit einer dreimal so langsamen Geschwindigkeit wie bei der Identität gegen den Uhrzeigersinn. Auch dies kann man am besten an den Höhenlinien sehen. Die geraden Höhenlinien korrespondieren wieder zur Höhe . |
 |
 |
Im Vergleich zur Funktion wurde der Funktionswert um verringert. Betrachten wir also den Realteil, so hat sich unsere Fläche um nach unten verschoben. Bei der Darstellung des Imaginärteils ist die reelle Zahl hingegen irrelevant und wir erhalten die gleiche Fläche wie zuvor beim Imaginärteil von . Allgemein können wir die Linearität des Realteils ausnützen und erhalten Vorlage:Einrücken Daraus folgt, dass die 3D-Animation dieser Funktion aus der Animation zur Kubikfunktion entsteht, indem die Fläche im Laufe der Zeit unterschiedlich stark nach oben oder unten verschoben wird. Am besten kann man das am Ursprung sehen, der kontinuierlich nach oben und unten wandert. Dieser ist cyan eingefärbt, da gilt. Wir können auch die drei Nullstellen von erkennen. Dies sind genau die dritten Einheitswurzeln (). Diese erscheinen als schwarze Punkte und bleiben auf fester Höhe, da dort die Höhenverschiebung durch die Drehung genau ausgeglichen wird. |
 |
 |
Die Funktion hat eine Polstelle bei . Wenn wir uns dieser Polstelle auf der positiven reellen Achse nähern, also für betrachten, so gilt . Dadurch entsteht der nach oben geöffnete Trichter. Nähern wir uns hingegen auf der negativen rellen Achse der , so gilt . Also bildet sich ein weiterer Trichter, der nach unten geöffnet ist. Es mag auf den ersten Blick verwirrend erscheinen, bei einer einzigen Polstelle zwei benachbarte Trichter zu sehen. In Wirklichkeit sind diese Trichter aber an der selben Position, nämlich bei . Es macht jedoch weder Sinn, als noch als anzusehen (noch als oder etwas anderes). Bei genauem Hinsehen erkennen wir auch, dass die Wand zwischen den beiden Trichtern eigentlich gar nicht existiert. Für betragsmäßig sehr große Eingabewerte wird der Funktionswert betragsmäßig sehr klein. Außerhalb der beiden Trichter wird unsere Fläche also immer flacher und nähert sich der --Ebene immer weiter an. Auch hier ist der -Teil nur eine gedrehte Variante des Realteils, aber dieses Mal erfolgt die Drehung im Uhrzeigersinn, denn Vorlage:Einrücken |
 |
 |
Blabla |
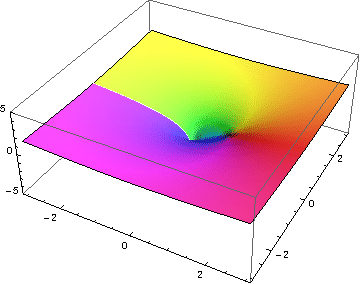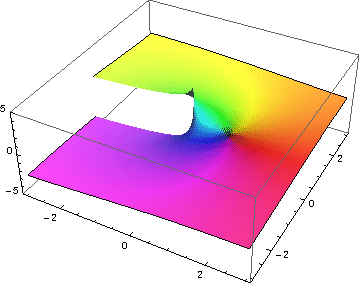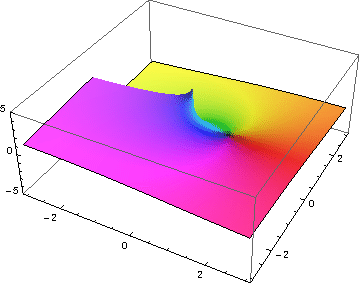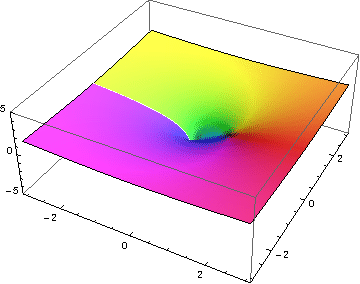 |
 |
Blabla |
 |
 |
Blabla |
 |
 |
Blabla |
 |
Bild kommt noch |
Blabla |
 |
Bild kommt noch |
Blabla |
Darstellung als Vektorfeld
Eine ganz andere Möglichkeit, sich eine Funktion zu veranschaulichen, ist die Darstellung über ein Vektorfeld. Dazu wählen wir in der komplexen Ebene ein regelmäßiges Punktgitter (beispielsweise alle Punkte mit ganzzahligen Koordinaten) und zeichnen an jedem Gitterpunkt einen Pfeil ein, der den Funktionswert an dieser Stelle darstellt. Dabei gibt die Richtung des Pfeils den Winkel und die Länge des Pfeils den Betrag des Funktionswerts an. Das sieht dann so aus:

Bei einer Nullstelle ist der Funktionswert und hat gar keine Richtung, sodass wir keinen Pfeil, sondern nur einen Punkt einzeichnen können.
Damit sich die Pfeile nicht überlappen, wählen wir für die Länge der Pfeile nicht den tatsächlichen Betrag des Funktionswerts, sondern skalieren die Pfeillängen so, dass der längste Pfeil höchstens so groß wie der Abstand zum nächsten Gitterpunkt ist. Um auch bei betragsmäßig kleinen Funktionswerten noch die Richtung der Pfeile erkennen zu können, verwenden wir eine logarithmische Skalierung. Bei den folgenden Bildern ist die Länge eines Pfeiles an der Stelle stets proportional zu (außer für ).
Beispiele
Vergleich der Visualisierungsmöglichkeiten
{{#invoke:Mathe für Nicht-Freaks/Seite|unten}}








































