Ing Mathematik: Grenzwerte und Stetigkeit

Aus der Schule wissen wir noch, dass wir nur stetige Funktionen ableiten konnten. Damals haben wir uns unter einer stetigen Funktion solche vorgestellt, die keine Sprünge oder Knicke hatten, die man "durchmalen" konnten. Wir werden den Begriff hier präzisieren und uns damit beschäftigen, wie wir die Stetigkeit bei einigen Funktionen zeigen können.

Stetigkeit

Wann ist jetzt eine Funktion stetig? Es gibt viele äquivalente Definitionen. Eine ursprüngliche und auch sehr anschauliche ist die sog. $\epsilon$-$\delta$-Definition, mit deren Aussage wir uns nur beschäftigen wollen. Sie besagt grob, dass sich bei einer kleinen Änderung des $x$-Wertes $f(x)$ sich ebenfalls nur wenig ändert. Genau heißt das, dass wenn wir im Punkt $x_0$ um unseren Funktionswert einen $\epsilon$-Kanal legen, es dann ein $\delta$ gibt, sodass alle Funktionswerte in diesem $\delta$-Intervall um $x_0$ auch in diesem $\epsilon$-Kanal liegen; dies muss für alle $\epsilon$ gelten.

Stetigkeit

Unstetigkeit

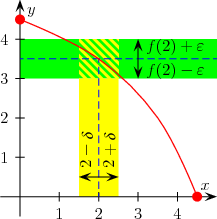
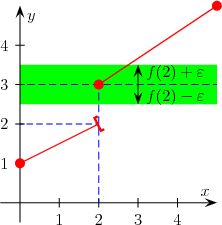
Diese Definition ist für kompliziertere Funktionen etwas unhandlich, man greift deshalb gerne oft auf die Definition über Folgen zurück.

Die Funktion y=f(x) heißt stetig an der Stelle $x_0$, wenn an dieser Stelle

1. ein endlicher Grenzwert existiert, und
2. dieser Grenzwert gleich dem Funktionswert ist.

Sind diese Bedingungen nicht erfüllt, so heißt die Funktion unstetig an der Stelle $x_0$. Dies ist dann der Fall, wenn

• die Funktion keinen Grenzwert besitzt.

oder

• die Funktion einen Grenzwert besitzt, aber $y_0\ne f(x_0)$ oder $f(x_0)$ ist nicht definiert. Man spricht hierbei auch von einer hebbaren Unstetigkeitsstelle $x_0$. Durch die Definition von $f(x_0)=\underset{x\to x_0}{\lim }f(x)$ kann die Funktion in $x_0$ stetig gemacht werden.

• Aber Achtung, nicht alles, was einen Knick hat, ist auch unstetig. Die Betragsfunktion ist überall stetig!

Grenzwert von Funktionen

Gegeben sei eine Funktion y=f(x). Weiters sei ein Punkt $x_0$ aus dem Definitionsbereich dieser Funktion gegeben. Nähert man sich mit x diesem Punkt beliebig weit an, so gibt es zwei Möglichkeiten:

1. f(x) nähert sich einem einem Wert $y_0=f\left(x_0\right)$
2. f(x) entspricht nicht $y_0=f\left(x_0\right)$.

Nur im ersten Fall existiert für y=f(x) ein Grenzwert (Limes) an der Stelle $x_0$

$\underset{x\to x_0}{\lim }f(x)=y_0$

Beispiel: Gegeben sei die Funktion $f(x)=\frac{1}{x}$. Gesucht ist der Grenzwert für $x_0=0$.

Nähert man sich $x_0$ von der linken Seite, so wird der linksseitige Grenzwert $f(x_0)=-\mathrm{\infty }$. Nähert man sich von rechts, so wird der rechtsseitige Grenzwert $f(x_0)=+\mathrm{\infty }$. Diese Funktion besitzt also für $x_0$ keinen Grenzwert.

Einseitiger Grenzwert

Schränkt man die Funktion ein auf Werte, die nur links von einer Stelle $x_0$ liegen und besitzt diese Teilfunktion dann an dieser Stelle einen Grenzwert, so besitzt die Funktion an dieser Stelle einen linksseitigen Grenzwert

$\underset{x\to x_o-}{\lim }f(x)$

Schränkt man die Funktion ein auf Werte, die nur rechts von einer Stelle $x_0$ liegen und besitzt diese Teilfunktion dann an dieser Stelle einen Grenzwert, so besitzt die Funktion an dieser Stelle einen rechtsseitigen Grenzwert.

$\underset{x\to x_o+}{\lim }f(x)$

Beispiel: Funktionen mit einer Sprungstelle besitzen dort zwar links- und rechtsseitige Grenzwerte, aber keinen Grenzwert.

Uneigentlicher Grenzwert

Ersetzt man $x_0$ durch $\mathrm{\infty }$ oder $-\mathrm{\infty }$ und existiert dort ein Grenzwert

$\underset{x\to \mathrm{\infty }}{\lim }f(x)$ oder $\underset{x\to -\mathrm{\infty }}{\lim }f(x)$

so spricht man von uneigentlichen Grenzwerten.

Beispiel: $\underset{x\to \mathrm{\infty }}{\lim }\frac{1}{x}=0$

Stückweise stetige Funktionen

Zwischenwertsatz für stetige Funktionen

Eine in einem Intervall [a,b] stetige Funktion f(x) nimmt jeden zwischen f(a) und f(b) gelegenen Wert mindestens einmal an.

Satz vom Minimum und Maximum

Eine in einem Intervall [a,b] stetige Funktion f(x) nimmt in diesem Intervall immer einen größten und einen kleinsten Wert an.

Infimum (Minimum): $f(x_1)=\underset{a\le x\le b}{\inf }f(x)$

Supremum (Maximum): $f(x_2)=\underset{a\le x\le b}{\sup }f(x)$

Übungen

Berechnen sie

• $\underset{x\to 4}{\lim }\frac{\sqrt{x}-1}{5-x^2}$
• $\underset{x\to -\mathrm{\infty }}{\lim }\frac{x}{1+x}$

Vorlage:Navigation zurückhochvor buch