Das Mehrkörperproblem in der Astronomie/ Hierarchische Algorithmen/ Zeitliche Hierarchie
Konstruktion
Wie soeben angedeutet, lassen sich die dynamischen Zeitskalen der Massenpunkte eines Mehrkörpersystems in eine hierarchische Struktur einordnen, indem man einen kleinsten elementaren Zeitschritt definiert und diesen sukzessive verdoppelt.

Um zu Beginn der Simulation festzulegen, muss man sich an der kleinsten anfänglich vorliegenden dynamischen Zeitskala orientieren. repräsentiert die Ebene 0, die niedrigste der Hierarchie. Durch Verdoppelung legt man die nächsthöhere Ebene 1 an, durch weitere Verdoppelung die Ebene 2 usw.
Fällt im Laufe der Modellierung die dynamische Zeitskala eines Körpers unter den Wert, welcher seine Zeitebene definiert, so muss er um eine Ebene nach unten geschoben werden. Tritt z.B. für ein Objekt auf Ebene 1 ein auf, so wechselt dieses zur Ebene 0. Wird sogar ein gefunden, so ist die bisherige elementare Schrittweite nicht länger gültig. An ihrer Stelle muss ein neuer Elementarschritt definiert werden, welcher fortan die Ebene 0 vertritt. Dementsprechend werden alle anderen Ebenen um 1 Niveau höher eingestuft. Aus der bisherigen Ebene 0 wird die Ebene 1, die bisherige Ebene 1 ist nun die Ebene 2 usw. Um zu vermeiden, dass diese Situation schon kurz nach dem Start der Simulation eintritt, empfiehlt es sich, zu Anfang so festzulegen, dass mit einem Betrag von genau zwischen und liegt.
Nimmt umgekehrt die dynamische Zeitskala so stark zu, dass sie den Wert der nächsthöheren Ebene überschreitet, gelangt der betroffene Massenpunkt um eine Stufe nach oben. Hat etwa ein Körper auf Ebene 1 ein , so steigt er zur Ebene 2 auf. Ein solches Höhersteigen ist nur zu solchen Zeitpunkten möglich, welche einem Vielfachen des auf der Zielebene gültigen Zeitschritts entsprechen, ein Wechsel z.B. von Ebene 1 zu Ebene 2 nur zu Zeitpunkten , , usw., nicht aber zu Zeitpunkten , usw. Ein aufsteigender Massenpunkt soll ja gleichzeitig mit den auf der Zielebene schon vorhandenen Objekten bewegt werden.
Ist auf der Ebene 0 kein Körper mehr vorhanden, so wird an Stelle von die auf der Ebene 1 gültige Schrittweite als neue elementare Schrittweite angesetzt. Sämtliche Ebenen werden dadurch um eine Stufe niedriger eingeordnet. Aus der bisherigen Ebene 1 wird eine Ebene 0, aus der Ebene 2 eine Ebene 1 usw.
Die höchste erforderliche Ebene richtet sich nach der größten im Ensemble auftretenden dynamischen Zeitskala . muss solange verdoppelt werden, bis die so erzeugte Zeitskala größer als die Hälfte von ist.
Wie die niedrigste ist auch die höchste Ebene dynamisch. Überschreitet für einen Massenpunkt das Doppelte der aktuell größten Zeitskala, so muss für diesen eine neue oberste Ebene angelegt werden. Wird die höchste Ebene nicht mehr benötigt, weil die dynamischen Zeitskalen aller Objekte unter der entsprechenden Schrittweite liegen, kann diese einfach entfernt werden.
Lösungsschema
Die Steigerung der Effizienz des Prädiktor-Korrektor-Algorithmus beruht darauf, nicht mehr die individuellen Zeitschritte der einzelnen Massenpunkte zu verwenden, sondern diejenigen , , usw. der Zeitebenen, auf welchen sich diese befinden. Da diese Schrittweiten nur einige wenige unterschiedliche Werte annehmen können, welche untereinander durch Verdoppelung hervorgehen, ist quasi automatisch sichergestellt, dass zumeist mehrere Körper den gleichen niedrigsten Wert aufweisen. Die sowieso immer erforderliche Extrapolation aller Positionen (und eventuell auch der Geschwindigkeiten) hin zu diesem Zeitpunkt kann so fast immer genutzt werden, um gleichzeitig mehrere Objekte zu bewegen. Das Lösungsschema sieht nun folgendermaßen aus:

1) Jeder Körper hat zum gegenwärtigen Zeitpunkt einen Zeitschritt . Die Ebene muss so gewählt werden, dass der individuelle Zeitschritt zwischen und liegt. Man greife diejenigen Massenpunkte heraus, welche gemeinsam für den niedrigsten Wert aufweisen (mittlere rote Kreise). Findet sich ausnahmsweise nur ein Objekt mit diesem Minimalwert, so wird wie bisher nur dieses als Einziges betrachtet.
Die aktuell zu bearbeitenden Massenpunkte lassen sich sehr einfach identifizieren, indem man die Simulation mit der zeitlichen Schrittweite ablaufen lässt. Objekte auf der Zeitebene 0 werden bei jedem Schritt bewegt, solche auf der Ebene 1 jeden 2. Schritt, solche auf der Ebene 2 jeden 4. Schritt usw.
2) Man wende unverändert den Prädiktor auf die Positionen aller Massenpunkte an, um die zum Zeitpunkt gültigen Positionen zu ermitteln (türkise Kreise). Mit den Hermite-Polynomen als grundlegendes Verfahren bestimme man entsprechend auch die Geschwindigkeiten .
3) Aus den Positionen gewinne man wie üblich die dazugehörigen Beschleunigungen für die ausgewählten Körper, im Falle der Hermite-Polynome als fundamentale Lösungsformel aus den und auch die Rucks .
4) Wie gehabt verbessere man die Positionen der gerade untersuchten Massenpunkte mit Hilfe des Korrektors und anschließend deren Geschwindigkeiten . Zuletzt aktualisiere man die Zeitebenen, auf welchen diese sich befinden. Falls erforderlich, führe man neue Ebenen ein oder entferne nicht mehr benötigte.
5) Abermals werden nur die in Schritt 1 ausgewählten Körper versetzt, alle anderen verbleiben auf ihren Positionen zum Zeitpunkt . Wieder kehre man zu Schritt 1 zurück.
Wie individuelle Zeitskalen pro Massenpunkt können auch hierarchische Schrittweiten auf jedes Prädiktor-Korrektor-Verfahren angewandt werden. Beispiele hierzu finden sich z.B. bei Makino (1991) [1] sowie Dehnen und Read (2011) [2]. Im Folgenden werden nur die auf die Hermite-Polynome sowie die Leapfrog-Methode beruhenden Lösungsschemata diskutiert. Das wiederum extrem unhandliche Mehrschritt-Verfahren ist zwar erneut etwas genauer, liefert aber keine grundlegend neuen Erkenntnisse über den Algorithmus.
Prädiktor-Korrektor-Verfahren mit hierarchischen Zeitschritten
Beispiel
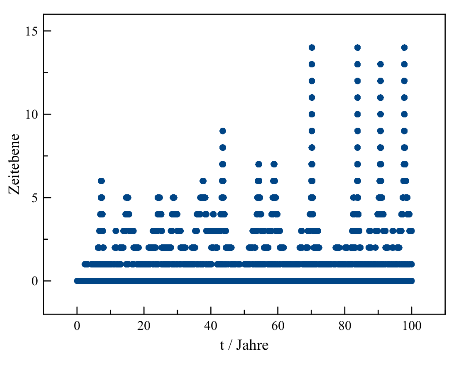
Eine Simulation mit hierarchischen Zeitschritten ist von gleicher Güte wie eine solche mit individuellen, wobei die Hermite-Polynome erwartungsgemäß erneut besser abschneiden als die Leapfrog-Methode. Betrachtet man abermals das schon mehrfach vorgeführte Drei-Körper-System, so befinden sich die jeweils nahestehenden Objekte zumeist beide auf der Zeitebene 0 und das dritte Mitglied auf einer höheren Ebene. Kommen sich zwei Massenpunkte sehr nahe, so wird der elementare Zeitschritt immer kleiner, was den dritten Körper (dessen dynamische Zeitskala absolut betrachtet nahezu unverändert bleibt) auf eine immer höhere Zeitebene gelangen lässt. Entfernen sich die Stoßpartner wieder voneinander, wird erneut größer, wodurch der dritte Massenpunkt auf niedrigere Ebenen zurückkehrt. Da falls erforderlich stets um den gleichbleibenden Faktor 2 geändert wird, erscheinen diese Anpassungen in logarithmischer Darstellung als Schritte konstanter Größe.