Physik Oberstufe/ Elektrizitätslehre/ Das magnetische Feld
Die Wechselwirkung von Magneten

Physik Oberstufe: Vorlage:Experiment-Box
Beschreibung durch Felder


Ein Magnet verändert den Raum in seiner Umgebung. Diese Raumänderung beschreiben wir durch ein Magnetfeld. Ein Magnetfeld an einem beliebigen Raumpunkt wird durch eine Magnetnadel nachgewiesen: Sie richtet sich im Feld aus. Physik Oberstufe: Vorlage:Experiment-Box Auch magnetische Felder veranschaulichen wir durch Feldlinien. Der Nordpol einer Magnetnadel zeigt immer in Richtung des Feldes, d.h. das Feld verläuft vom magnetischen Nord- zum Südpol.
Das Feld stromdurchflossener Leiter
Gerader Leiter
Physik Oberstufe: Vorlage:Experiment-Box

Zur Bestimmung der Magnetfeldrichtung um einen stromdurchflossenen Leiter dient die „Rechte-Faust-Regel“:
- Daumen: Stromrichtung (definiert als die Bewegungsrichtung positiver Ladungsträger)
- gekrümmte Finger: Feldrichtung
Der Vollständigkeit halber soll hier noch die Formel, die man für die Abhängigkeit der Stärke des Magnetfelds vom Radius findet, angegeben werden: Physik Oberstufe: Vorlage:Hervorhebung
Aufgabe: Magnetfelder um stromdurchflossene Leiter.
Spule

Wir können den Leiter in vielen Windungen aufwickeln und erhalten eine Spule. Im Inneren der Spule verstärken sich die Felder der einzelnen Windungen und wir erhalten einen Elektromagneten. Bei einer langen Spule herrscht im Inneren ein homogenes Feld, außerhalb das Feld eines Stabmagneten.
Ein Maß für die Stärke des Magnetfelds
Datei:Leiterschaukelversuch.ogv Wir suchen ein Maß für die Stärke des Magnetfelds vergleichbar mit der Stärke des elektrischen Feldes:
- .
Eine analoge Definition ist aber nicht möglich, da es keine magnetischen Monopole gibt.

Physik Oberstufe: Vorlage:Experiment-Box
Die Größe definiert als:
Physik Oberstufe: Vorlage:Hervorhebung
heißt magnetische Induktion oder auch Kraftflussdichte. Sie hat die Einheit:
Dabei ist die Kraft auf ein Rähmchen der Breite und der Windungszahl , durch das der Strom fließt und das sich senkrecht zu den Feldlinien befindet.
Aufgabe: Wie geht man vor, wenn der Leiter nicht senkrecht auf den Feldlinien steht?
Das Magnetfeld der langen Spule

Gesucht ist eine Formel zur Bestimmung des Magnetfelds im Innern einer langen Spule. Wovon könnte abhängen?
- Windungszahl
- Stromstärke
- Länge der Spule
- Querschnittsfläche
- Material in der Spule
Physik Oberstufe: Vorlage:Experiment-Box
Physik Oberstufe: Vorlage:Hervorhebung
Dabei ist die magnetische Feldkonstante:
Physik Oberstufe: Vorlage:Hervorhebung
Das Material in der Spule wird mit der Permeabilitätszahl berücksichtigt.
Aufgabe: Elektrisches und magnetisches Feld im Vergleich.
Dia-, Para-, und Ferromagnetismus

Es gilt für die Feldstärke des äußeren Feldes H, d.h. bei einer langen Spule:
und damit für die Flussdichte des induzierten Feldes B:
.
Man beobachtet bei einigen Stoffen, den ferromagnetischen Stoffen, einen starken Einfluss auf Magnetfelder. Bei genauerer Untersuchung kann man Stoffe (oder besser: die in ihnen vorhandenen/dominierenden Effekte) u.a. in die Kategorien des Dia-, Para-, und Ferromagnetismus einteilen.
Wir beschreiben diese Effekte durch die Permeabilitätszahl , die die Magnetisierung eines Materials in einem äußeren Magnetfeld angibt.
Stoffe, deren Atome, Ionen oder Moleküle keine ungepaarten Elektronen besitzen, haben keine eigenen magnetischen Momente. Im Magnetfeld werden aber Ströme induziert, die ihrer Ursache entgegen wirken (Lenzsche Regel) und das Magnetfeld demnach (meist in geringem Maße) abschwächen.

Die meisten Materialien besitzen bereits kleine atomare magnetische Momente, die aber in alle möglichen Richtungen zeigen. Im Mittel gleichen sich diese also aus und die Stoffe sind nicht magnetisch. Bringt man sie aber in ein Magnetfeld, so richten sich die vorhandenen magnetischen Momente (teilweise) aus und verstärken dadurch das äußere Magnetfeld (meist geringfügig).
Ferromagnetische Stoffe (Eisen und Ferrite, Cobalt, Nickel) besitzen ebenfalls eigene magnetische Momente die sich im äußeren Magnetfeld ausrichten. Aufgrund quantenmechanischer Effekte im Festkörper erfolgt die Ausrichtung aber in einer viel stärkeren Weise als bei paramagnetischen Stoffen, wodurch sehr große Permeabilitätszahlen resultieren (siehe Tabelle).
 |
 |
Hysterese
Die Lorentzkraft

Bestimmung der Lorentzkraft
Physik Oberstufe: Vorlage:Experiment-Box
ToDo Bild
Es gilt mit , der Anzahl der bewegten Elektronen im Leiter:
Bestimmung der Anzahl der bewegten Elektronen

Es ist
die Bewegte Ladung im Leiter, wobei die Zeit ist, die ein Elektron braucht, um den Leiter zu durchwandern:
Damit folgt:
und für die Lorentzkraft erhält man:
Physik Oberstufe: Vorlage:Hervorhebung Richtung der Kraft: Drei-Finger-Regel (UVW), die Lorentzkraft steht immer senkrecht zur Richtung des Magnetfelds und senkrecht zur Richtung der Geschwindigkeit .
Bewegung von Ladungen im Magnetfeld
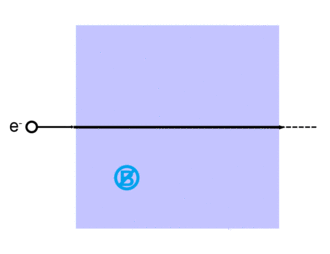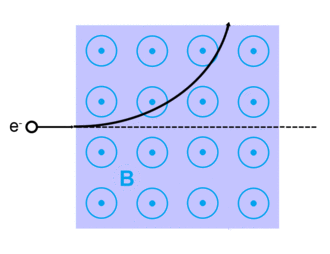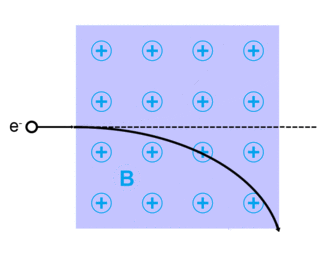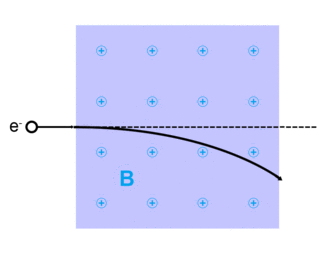

Physik Oberstufe: Vorlage:Experiment-Box
Aus der Beschleunigungsspannung , der Magnetfeldstärke und dem Radius der Kreisbahn können wir den Quotienten , die sog. spezifische Ladung des Elektrons, bestimmen:
Kennt man die Elektronenladung aus dem Millikanversuch, so kann man nun die Elektronenmasse bestimmen.
Aufgabe: Elektronenstrahl im magnetischen Feld.
Massenspektrometrie


Die Ablenkung geladener und sich bewegender Teilchen in elektrischen und magnetischen Feldern kann man ausnutzen, um den Quotienten und damit bei Kenntnis der Ladung die Masse von Teilchen zu ermitteln.
Je nach Anwendungsfall ist es erforderlich, die Teilchen zuerst durch einen Geschwindigkeitsfilter laufen zu lassen, der nur Teilchen mit der gleichen Geschwindigkeit hindurch lässt. Anschließend misst man die Ablenkung im Magnetfeld und berechnet daraus die gesuchte Größe.






