Mathe für Nicht-Freaks: Eigenschaften des Sinus und Kosinus

{{#invoke:Mathe für Nicht-Freaks/Seite|oben}}

Additionstheoreme

Im Folgenden untersuchen wir die Additionstheoreme. Diese befassen sich mit $\sin (x+y)$ beziehungsweise $\cos (x+y)$ für $x,y\in ℝ$. Veranschaulichen können wir uns diesen Satz, indem wir Sinus und Kosinus am Einheitskreis betrachten.

Trigonometrischer Pythagoras

Wir wollen nun eine der wichtigsten Identitäten von Sinus und Kosinus betrachten. Vorlage:Todo

Mathe für Nicht-Freaks: Vorlage:Satz Man kann den Satz ebenso beweisen, indem man Sinus und Kosinus mit der Exponentialfunktion ausdrückt und dann die linke Seite ausrechnet: Mathe für Nicht-Freaks: Vorlage:Alternativer Beweis

Definition von $\pi$

Im letzten Kapitel haben wir Sinus und Kosinus sowohl anschaulich als Funktion eines Winkels definiert, als auch analytisch über eine Reihe bzw. über die Exponentialfunktion. Wie du vielleicht noch aus der Schule weißt, wird bei der ersten Definition der Winkel im Bogenmaß gemessen. Zum Beispiel hat ein rechter Winkel die Größe $90^{\circ }=\frac{\pi }{2}$, denn wenn man aus dem Einheitskreis einen Viertelkreis herausschneidet, hat dieser die Länge $\frac{\pi }{2}$. Somit ist auch anschaulich klar, dass $\cos (\frac{\pi }{2})=0$ gilt.

Ein Grund der rein analytischen Definition von Sinus und Kosinus ist, die Werte der Sinus- und Kosinusfunktion mathematisch präzise festzulegen, ohne auf die geometrische Anschauung zurückgreifen zu müssen. Daher macht es Sinn, auch die berühmte Kreiszahl $\pi$ rein analytisch zu definieren. Die bekannte Definition von $\pi$ als Verhältnis von Umfang zu Durchmesser eines Kreises erweist sich nämlich in der Analysis als nicht geeignet zur strengen Beweisführung.

Die Idee ist nun, $\pi$ einfach so zu definieren, dass $\cos (\frac{\pi }{2})=0$ gilt. Genauer gesagt wollen wir festlegen, dass $\frac{\pi }{2}$ die kleinste positive Nullstelle des Kosinus sein soll ($\pi$ ist dann das Doppelte davon). Damit diese Definition funktioniert, müssen wir aber erst beweisen, dass eine kleinste solche Nullstelle überhaupt existiert.

Jetzt können wir endlich $\pi$ definieren.

Die Existenz dieses Minimums war gerade die Aussage des vorangegangenen Satzes. Aus dem Beweis dieses Satzes geht auch hervor, dass $\frac{\pi }{2}<2$ gilt. Wir haben also $0<\pi <4$.

Qualitatives Verhalten der Kosinusfunktion

Dass $\frac{\pi }{2}$ die kleinste positive Nullstelle des Kosinus ist, hat eine Fülle von Aussagen über die Kosinusfunktion zur Folge, die es uns erlaubt, ein vollständiges Bild vom qualitativen Verhalten der Kosinusfunktion zu bekommen. Insbesondere werden wir zeigen, dass $\cos :[0,\frac{\pi }{2}]\to [0,1]$ bijektiv und streng monoton fallend ist und dass die Funktionswerte auf ganz $ℝ$ unmittelbar aus den Funktionswerten auf $[0,\frac{\pi }{2}]$ hervorgehen.

Verhalten auf $[0,\frac{\pi }{2}]$

Die Kosinusfunktion auf dem Intervall $[0,\frac{\pi }{2}]$

Aus dem trigonometrischen Pythagoras folgt ${\cos }^2(x)\in [0,1]$, also $\cos (x)\in [-1,1]$, sodass wir den Kosinus als Funktion $\cos :ℝ\to [-1,1]$ auffassen können. Wäre $\cos (x)<0$ für ein $x\in [0,\frac{\pi }{2}]$, so gäbe es wegen $\cos (0)=1>0$ nach dem Zwischenwertsatz ein $0<\xi <x\le \frac{\pi }{2}$ mit $\cos (\xi )=0$, doch das steht im Widerspruch dazu, dass $\frac{\pi }{2}$ die kleinste positive Nullstelle des Kosinus ist. Also können wir die Einschränkung des Kosinus auf das Intervall $[0,\frac{\pi }{2}]$ sogar als Funktion $\cos :[0,\frac{\pi }{2}]\to [0,1]$ auffassen. Wir zeigen nun, dass diese Einschränkung bijektiv und streng monoton fallend ist. Mathe für Nicht-Freaks: Vorlage:Satz

Fortsetzung auf $[\frac{\pi }{2},\pi ]$

Wir stellen zunächst fest, dass sich aus $\cos (\frac{\pi }{2})=0$ folgender Zusammenhang ergibt, den man als eine Punktsymmetrie der Kosinusfunktion um die Stelle $\frac{\pi }{2}$ beschreiben könnte. Mathe für Nicht-Freaks: Vorlage:Satz Indem wir $x\in [0,\frac{\pi }{2}]$ in diesem Satz wählen, erkennen wir, dass die Einschränkung des Kosinus auf das Intervall $[\frac{\pi }{2},\pi ]$ eine Funktion $\cos :[\frac{\pi }{2},\pi ]\to [-1,0]$ darstellt, die erneut bijektiv und streng monoton fallend ist.

Die Kosinusfunktion auf dem Intervall $[0,\pi ]$ geht aus der Kosinusfunktion auf dem Intervall $[0,\frac{\pi }{2}]$ hervor

Insgesamt ergibt sich also: Mathe für Nicht-Freaks: Vorlage:Satz Dieser Satz wird bei der Definition des Arkuskosinus eine wichtige Rolle spielen.

Fortsetzung auf $[\pi ,2\pi ]$

Im Weiteren wird sich eine andere Formulierung des obigen Zusammenhangs als nützlich erweisen. Mathe für Nicht-Freaks: Vorlage:Satz Indem wir nun $x\in [0,\pi ]$ wählen, sehen wir, dass auf dem Intervall $[\pi ,2\pi ]$ die entsprechenden Werte auf dem Intervall $[0,\pi ]$ lediglich gespiegelt werden.

Die Kosinusfunktion auf dem Intervall $[0,2\pi ]$ geht aus der Kosinusfunktion auf dem Intervall $[0,\pi ]$ hervor

Die Einschränkungen $\cos :[\pi ,\frac{3\pi }{2}]\to [-1,0]$ und $\cos :[\frac{3\pi }{2},2\pi ]\to [0,1]$ sind also jeweils bijektiv und streng monoton steigend.

Fortsetzung auf $ℝ$

Es stellt sich nun heraus, dass die Kosinusfunktion periodisch ist: Mathe für Nicht-Freaks: Vorlage:Satz Auf den Intervallen $\dots ,[-4\pi ,-2\pi ],[-2\pi ,0],[0,2\pi ],[2\pi ,4\pi ],[4\pi ,6\pi ],\dots$ verhält sich der Kosinus also jeweils exakt so, wie wir es bereits für das Intervall $[0,2\pi ]$ untersucht haben.

Die Kosinusfunktion geht aus der Kosinusfunktion auf dem Intervall $[0,2\pi ]$ hervor

Mit anderen Worten: Mathe für Nicht-Freaks: Vorlage:Satz

Die folgende Grafik veranschaulicht noch einmal, wie sich alle Funktionswerte des Kosinus auf die Werte im Intervall $[0,\frac{\pi }{2}]$ zurückführen lassen.

Die Kosinusfunktion geht aus der Kosinusfunktion auf dem Intervall $[0,\frac{\pi }{2}]$ hervor

Nullstellen, Maxima und Minima

Der vorangegangene Satz erlaubt es uns zu bestimmen, wo die Nullstellen, Maxima und Minima liegen, also die Funktionswerte $0$, $1$ und $-1$ angenommen werden. Mathe für Nicht-Freaks: Vorlage:Satz Vorlage:Todo

Periodizität

Wir haben bereits gezeigt, dass $\cos (x+2\pi )=\cos (x)$ für alle $x\in ℝ$ gilt. Wir beweisen jetzt, dass $2\pi$ die kleinste Zahl mit dieser Eigenschaft ist. Daher macht es Sinn, den Kosinus als $2\pi$-periodische Funktion zu bezeichnen. Mathe für Nicht-Freaks: Vorlage:Satz Alle möglichen Periodenlängen sind also Vielfache von $2\pi$, womit $2\pi$ die kleinste Periodenlänge ist.

Qualitatives Verhalten der Sinusfunktion

In diesem Abschnitt werden wir erkennen, dass die Sinusfunktion lediglich eine Verschiebung der Kosinusfunktion ist. Auf diese Weise lassen sich alle Eigenschaften der Kosinusfunktion aus dem vorherigen Abschnitt leicht auf die Sinusfunktion übertragen.

Funktionswert bei $\frac{\pi }{2}$

Wir überlegen uns zunächst, was $\sin (\frac{\pi }{2})$ ist. Da $\cos (\frac{\pi }{2})=0$ gilt, folgt aus dem trigonometrischen Pythagoras sofort ${\sin }^2(\frac{\pi }{2})=1$. Es gilt also entweder $\sin (\frac{\pi }{2})=1$ oder $\sin (\frac{\pi }{2})=-1$. Um Letzteres auszuschließen, treffen wir für $0<x<2$ folgende Abschätzung: Vorlage:Einrücken Wir wissen ja, dass $0<\frac{\pi }{2}<2$ gilt. Somit ist $\sin (\frac{\pi }{2})>0$ und es folgt $\sin (\frac{\pi }{2})=1$.

Zusammenhang zur Kosinusfunktion

Mathe für Nicht-Freaks: Vorlage:Satz Der Graph der Sinusfunktion (rot) entsteht also aus dem Graphen durch Kosinusfunktion (blau) durch eine Verschiebung um $\frac{\pi }{2}$ nach rechts.

Übergang von Kosinus zu Sinus und umgekehrt

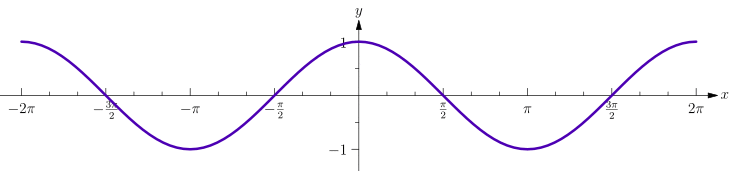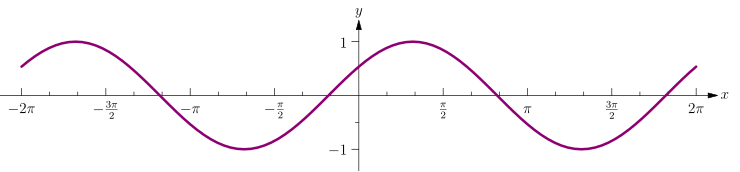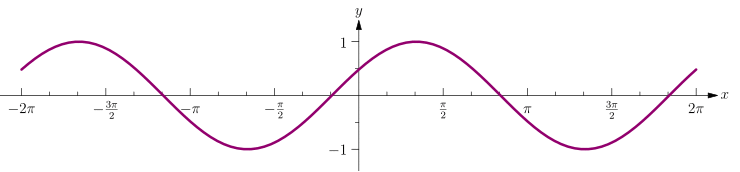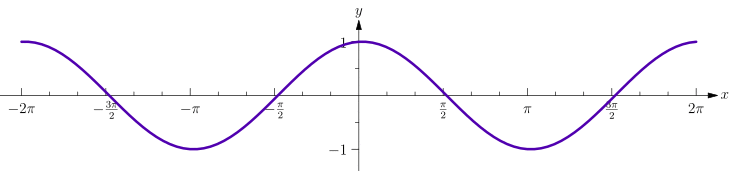
Verhalten auf $ℝ$

Da der Sinus nur ein verschobener Kosinus ist, können wir das qualitative Verhalten der Sinusfunktion auf ganz $ℝ$ leicht bestimmen. Mathe für Nicht-Freaks: Vorlage:Satz Vorlage:Todo

Nullstellen, Maxima und Minima

Ebenso leicht lässt sich die Bestimmung von Nullstellen, Maxima und Minima auf die Sinusfunktion übertragen, denn deren Lage verschiebt sich lediglich um $\frac{\pi }{2}$ nach rechts. Mathe für Nicht-Freaks: Vorlage:Satz Vorlage:Todo

Ableitung und Integral

Ableitung Sinus

{{#lst:Mathe für Nicht-Freaks: Beispiele für Ableitungen|Satz:Ableitung Sinus}}

Ableitung Kosinus

{{#lst:Mathe für Nicht-Freaks: Beispiele für Ableitungen|Satz:Ableitung Kosinus}}

{{#invoke:Mathe für Nicht-Freaks/Seite|unten}}