Datei:01 Quadratur des Kreises E-8.svg

Diese Datei stammt aus Wikimedia Commons und kann von anderen Projekten verwendet werden. Die Beschreibung von deren Dateibeschreibungsseite wird unten angezeigt.
Beschreibung
| Beschreibung01 Quadratur des Kreises E-8.svg |
Deutsch: Quadratur des Kreises, Näherungskonstruktion mithilfe
 English: Squaring the circle, approximate construction with help  |
| Datum | |
| Quelle | Eigenes Werk |
| Urheber | Petrus3743 |
| SVG‑Erstellung InfoField |
Anmerkung
Die Näherung von 
Die Verwendung der Quadratwurzel aus 2 = 


- Ergebnis der folgenden Konstruktion
- Ergebnis mit Zu Chongzhi-Bruch
Konstruktion

 als Animation, in 13 Schritten bis a / 2, zweimal 10 sec Pause
als Animation, in 13 Schritten bis a / 2, zweimal 10 sec Pause- Ziehe einen Kreis mit beliebigem Radius
um seinen Mittelpunkt
- Zeichne das Quadrat
mit
als Seitenlänge und verlängere die Strecke
über
hinaus.
- Ziehe die Diagonale
ergibt Schnittpunkt
- Zeichne eine Parallele zu
durch
bis
ergibt Schnittpunkt
- Ziehe einen Halbkreis um
ab
im Uhrzeigersinn, ergibt Schnittpunkt
- Halbiere die Strecke
in
- Verbinde
mit
ergibt Schnittpunkt
- Bestimme den Punkt
so, dass
- Verbinde
mit
ergibt Schnittpunkt
- Zeichne eine Parallele zu
ab
bis Strecke
ergibt Schnittpunkt
Wird die Strecke 

Fehler
Bei einem Kreis mit Radius r = 1 [LE]:
- Konstruierte Seite des Quadrates a = 1,772453865554221... [LE]
- Soll-Seite des Quadrates as =
= 1,772453850905516... [LE]
- Absoluter Fehler = a - as = 0,000000014648705... = 1,4648...E-8 [LE]
- Fläche des konstruierten Quadrates A = a2 = 3,141592705518100... [FE]
- Soll-Fläche des Quadrates As =
= 3,141592653589793... [FE]
- Absoluter Fehler = A - As = 0,000000051928307... = 5,1928...E-8 [FE]
- Fazit: Sieben Nachkommastellen sind gleich denen von
bzw. sechs Nachkommastellen sind gleich denen von
.
- Bei einem Kreis mit dem Radius r = 100 km wäre der Fehler der Seite a ≈ 1,5 mm
- Bei einem Kreis mit dem Radius r = 10 m wäre der Fehler der Fläche A ≈ 5,2 mm2
Annotation
The approximation of 
The use of the square root of 2 = 


- Result of the following construction
- Result with Zu Chongzhi fraction
Construction

 as animation, in 13 steps till a/2, twice 10 second pause
as animation, in 13 steps till a/2, twice 10 second pause- Draw a circle with any radius
around its center
- Draw the square
with
as the side length and extend the line segment
beyond
- Draw the diagonal
results in intersection point
- Draw a parallel to
through
to
results in intersection
- Draw a semicircle around
clockwise, results in intersection point
- Halve the line segment
in
- Connect
to
results in intersection
- Find the point
such that
- Connect
to
results in intersection point
- Draw a parallel to
from
to line segment
results in intersection
If the line segment 

Error
In a circle of radius r = 1 [unit length, ul]:
- Constructed side of the square a = 1.772453865554221... [
]
- Target side of the square as =
= 1.772453850905516... [
]
- Absolute error = a - as = 0.000000014648705... = 1.4648...E-8 [
]
- Surface of the constructed square A = a2 = 3.141592705518100... [unit area, ua]
- Target area of the square As =
= 3.141592653589793... [
]
- Absolute error = A - As = 0.000000051928307... = 5.1928...E-8 [
]
- Conclusion: seven decimal places are equal to those of
respectively six decimal places are equal to those of
.
- In a circle of radius r = 100 km would be the fault of the page a ≈ 1.5 mm
- In the case of a circle with the radius r = 10 m would be the error of the surface A ≈ 5.2 mm2
Lizenz
- Dieses Werk darf von dir
- verbreitet werden – vervielfältigt, verbreitet und öffentlich zugänglich gemacht werden
- neu zusammengestellt werden – abgewandelt und bearbeitet werden
- Zu den folgenden Bedingungen:
- Namensnennung – Du musst angemessene Urheber- und Rechteangaben machen, einen Link zur Lizenz beifügen und angeben, ob Änderungen vorgenommen wurden. Diese Angaben dürfen in jeder angemessenen Art und Weise gemacht werden, allerdings nicht so, dass der Eindruck entsteht, der Lizenzgeber unterstütze gerade dich oder deine Nutzung besonders.
- Weitergabe unter gleichen Bedingungen – Wenn du das Material wiedermischst, transformierst oder darauf aufbaust, musst du deine Beiträge unter der gleichen oder einer kompatiblen Lizenz wie das Original verbreiten.
Kurzbeschreibungen
In dieser Datei abgebildete Objekte
Motiv
Einige Werte ohne einen Wikidata-Eintrag
27. Dezember 2019
image/svg+xml
3f36dbb17098206bb2340fde0386aa5d7e1f5f55
10.163 Byte
605 Pixel
608 Pixel
Dateiversionen
Klicke auf einen Zeitpunkt, um diese Version zu laden.
| Version vom | Vorschaubild | Maße | Benutzer | Kommentar | |
|---|---|---|---|---|---|
| aktuell | 18:43, 23. Jun. 2022 | 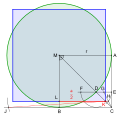 | 608 × 605 (10 KB) | wikimediacommons>Petrus3743 | Vereinfachung |
Dateiverwendung
Die folgende Seite verwendet diese Datei:
![{\displaystyle {\overline {KL}}={\frac {a}{2}}=1-{\frac {{\sqrt {2}}\left(2-{\sqrt {2}}\right)\left(2-{\sqrt {2}}+{\sqrt {{\frac {1}{2}}+{\sqrt {2}}}}\right)}{-11+11{\sqrt {2}}+5{\sqrt {1+2{\sqrt {2}}}}}}\approx r\cdot \ 0{,}886\;226\;932\;777\;110\;[\mathrm {LE} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da96da4ffd59dc73ae1e96655d160ac14772adf6)













![{\displaystyle {\overline {KL}}={\frac {a}{2}}=1-{\frac {{\sqrt {2}}\left(2-{\sqrt {2}}\right)\left(2-{\sqrt {2}}+{\sqrt {{\frac {1}{2}}+{\sqrt {2}}}}\right)}{-11+11{\sqrt {2}}+5{\sqrt {1+2{\sqrt {2}}}}}}\approx r\cdot \ 0.886\;226\;932\;777\;110\;[\mathrm {ul} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e227646be0d1a7d383909880453b35c75254fb4)


