Datei:01 Dreiteilung des Winkels-180°-2.svg

Diese Datei stammt aus Wikimedia Commons und kann von anderen Projekten verwendet werden. Die Beschreibung von deren Dateibeschreibungsseite wird unten angezeigt.
Beschreibung
| Beschreibung01 Dreiteilung des Winkels-180°-2.svg |
Deutsch: Dreiteilung des Winkels mit Kurzbeschreibung, Näherungskonstruktion für Winkel zwischen 0° und 180°. Ein paar Konstruktionselemente stammen aus Alberts' Konstruktion.
English: Trisection of an angle with brief description, proximity construction for angles between 0° and 180°. A few construction elements come from Alberts' construction. |
| Datum | |
| Quelle | Eigenes Werk |
| Urheber | Petrus3743 |
| Andere Versionen |
 Trisection of an angle, proximity construction for angles between 0° and 180°, as an animation with step sizes approx. 3° to 4°, for reasons of clarity the points are without labeling.  Trisection of an angle with brief description, proximity construction for angles between > 0° and 180°. A few construction elements come from Alberts' construction. |
| SVG‑Erstellung InfoField |
Anmerkungen
Mit der stark vereinfachten Konstruktion wird folgendes erreicht:
- Ein großer Teil der Konstruktion liegt in der unteren Hälfte des Kreises
- Eine praktikable Dreiteilung des Winkels ab nahe
bis
Siehe hierzu in GeoGebra
Konstruktion


- Kreis
mit beliebigem Durchmesser
um Mittelpunkt
- Winkelschenkel
und Winkelschenkel
schließen den Winkel
im Scheitel
ein,
und
den Ergänzungswinkel
- Kreis
um
mit Radius
; die Verlängerung des Winkelschenkels
schneidet Kreis
in
- Durchmesser
mit
und Verbindung des Punktes
mit
- Punkt
auf Kreis
so, dass
- Strecke
in
halbieren, die anschließende Mittelsenkrechte von
schneidet
in
ergibt
- Parallele zu
ab
erreicht Kreis
in
- Parallele zu
ab
Punkt
darauf so, dass
- Linie ab
durch
erreicht Kreis
in
anschließend Linie ab
bis
- Parallele zu
ab
erreicht Kreis
in
- Strecke
über
hinaus verlängern, Punkt
darauf so, dass
- Linie ab
durch
erreicht Kreis
in
- Bestimme Punkt
so, dass Winkel
Verbindung
mit
ergibt den Winkel
- Mittelsenkrechte von
schneidet
in
verbinde
mit
- Bestimme Punkt
so, dass Winkel
- Abschließende Verbindung
mit
ergibt Winkel
- Der Winkel
ist nahezu gleich einem Drittel des Winkels
- Der Winkel
ist nahezu gleich einem Drittel des Winkels
Fehlerbetrachtung
Eine Fehleranalyse, ähnlich Alberts' Konstruktion, ist nicht vorhanden.
Die dargestellte Konstruktion wurde mit der Dynamische-Geometrie-Software (DGS) GeoGebra angefertigt; darin werden in diesem Fall die Winkelgrade meist mit signifikanten dreizehn Nachkommastellen angezeigt. Die sehr kleinen Fehler des Winkels 




Betrachtet man die Grafik in GeoGebra, in sehr kleinen Schritten, die zu- oder abnehmenden Winkelweiten des Winkels 




Verdeutlichung des absoluten Fehlers
Der in GeoGebra ablesbare Differenzwert von max. 



Hätten die Winkelschenkel die Länge gleich 1 Milliarde km (das Licht bräuchte für diese Strecke ≈ 56 Minuten, das ist etwas weniger als 7-mal die Entfernung Erde – Sonne), wäre der absolute Fehler der beiden – nicht eingezeichneten – Sehnen 

Fehlerüberprüfung eines frei gewählten Winkels > 0° ... 180°
- Siehe GeoGebra
Remarks
With the greatly simplified construction, the following is achieved:
- Much of the construction is in the lower half of the circle
- A practical trisection of the angle from close
to
See also in GeoGebra
Construction


- Circle
with any diameter
around center
- Angle leg
and angle leg
enclose the angle
in apex
,
and
the supplementary angle
- Circle
around
with radius
the extension of the angle leg
intersects circle
in
- Diameter
with
and connection of point
with
- Point
on circle
so that
- Line segment
in
halved, the perpendicular bisector of
cuts
in
results
- Parallel to
from
reaches circle
in
- Parallel to
from
point
on it such that
- Line from
through
reaches circle
in
then line from
to
- Parallel to
from
reaches circle
in
- Line segment
extended beyond
, point
on it that
- Line from
through
reaches circle
in
- Determine point
so that angle
connection
with
gives the angle
- Perpendicular bisector of
cuts
in
connect
with
- Determine point
so that angle
- Final connection
with
gives angle
- The angle
is almost equal to one third of the angle
- The angle
is almost equal to a third of the angle
Error viewing
An error analysis, similar to Alberts' construction, is not available.
The construction shown was made with the dynamic geometry software (DGS) GeoGebra; in this case the degrees are usually displayed with significant thirteen decimal places. The very small errors of the angle 




If you look at the graphic in GeoGebra, in very small steps, the increasing or decreasing angular widths of the angle 




Clarification of the absolute error
The difference value shown in GeoGebra of max. 



If the angled legs had a length of 1 Billion km (the light would need ≈ 56 minutes for this distance, that's a little less than 7 times the distance earth - sun.), the absolute error of the twoden – not shown – cords would be 

Trisection an angle > 0° ... 180°, for checking the error
- See GeoGebra
Lizenz
- Dieses Werk darf von dir
- verbreitet werden – vervielfältigt, verbreitet und öffentlich zugänglich gemacht werden
- neu zusammengestellt werden – abgewandelt und bearbeitet werden
- Zu den folgenden Bedingungen:
- Namensnennung – Du musst angemessene Urheber- und Rechteangaben machen, einen Link zur Lizenz beifügen und angeben, ob Änderungen vorgenommen wurden. Diese Angaben dürfen in jeder angemessenen Art und Weise gemacht werden, allerdings nicht so, dass der Eindruck entsteht, der Lizenzgeber unterstütze gerade dich oder deine Nutzung besonders.
- Weitergabe unter gleichen Bedingungen – Wenn du das Material wiedermischst, transformierst oder darauf aufbaust, musst du deine Beiträge unter der gleichen oder einer kompatiblen Lizenz wie das Original verbreiten.
Die Methode basiert in einigen Konstruktionselementen auf Alberts' Konstruktion.
Kurzbeschreibungen
In dieser Datei abgebildete Objekte
Motiv
Einige Werte ohne einen Wikidata-Eintrag
7. März 2020
image/svg+xml
b52a6790cd5b4fb0762d009cab7d68432a7f4fe9
292.530 Byte
471 Pixel
703 Pixel
Dateiversionen
Klicke auf einen Zeitpunkt, um diese Version zu laden.
| Version vom | Vorschaubild | Maße | Benutzer | Kommentar | |
|---|---|---|---|---|---|
| aktuell | 20:03, 11. Jan. 2021 | 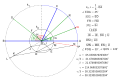 | 703 × 471 (286 KB) | wikimediacommons>Petrus3743 | Grafikfehler korr. |
Dateiverwendung
Die folgenden 2 Seiten verwenden diese Datei:

















![{\displaystyle F=2\cdot \sin \left({\frac {1\cdot 10^{-13}\mathrm {^{\circ }} }{2}}\right)=0{,}000\;000\;000\;000\;001\;745\ldots =1{,}745\ldots \cdot 10^{-15}\;[\mathrm {LE} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12684260ede34dd5c2cda172dd4e5032324a8a43)
![{\displaystyle F=2\cdot \sin \left({\frac {1\cdot 10^{-13}\mathrm {^{\circ }} }{2}}\right)=0.000\;000\;000\;000\;001\;745\ldots =1.745\ldots \cdot 10^{-15}\;[\mathrm {unit\;of\;length} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa66a5e9ee1c01580c05d90f8f7b546fdaad605a)