Formelsammlung Mathematik: Geometrie

Zurück zu Formelsammlung_Mathematik

Planimetrie

Dreiecke

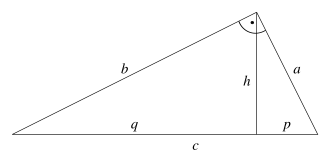
Rechtwinkliges Dreieck

Satz des Pythagoras

Die allgemeine Aussage des Satzes des Pythagoras lautet:

In einem rechtwinkligen Dreieck ist das Quadrat über der Hypotenuse gleich der Summe der Quadrate über den beiden Katheten.

$c^2=a^2+b^2$

Satz: Die Summe der Quadrate über den Katheten ist gleich dem Quadrat über der Hypotenuse.

Daraus folgt:

Kathetensatz des Euklid

Im rechtwinkligen Dreieck gilt

$a^2=p\cdot c$ $b^2=q\cdot c$

Rechtwinkliges Dreieck mit Höhe h

Höhensatz des Euklid

Im rechtwinkligen Dreieck gilt

$h^2=p\cdot q$

---

Sinussatz

$\frac{a}{\sin \alpha }=\frac{b}{\sin \beta }=\frac{c}{\sin \gamma }$

Kosinussatz

$a^2=b^2+c^2-2\cdot b\cdot c\cdot \cos \alpha$

$\cos \alpha =\frac{b^2+c^2-a^2}{2\cdot b\cdot c}$

Winkelsumme

• Die Winkelsumme im Dreieck beträgt 180°.

gleichseitiges Dreieck

Für ein gleichseitiges Dreieck der Seitenlänge a gilt:

• Alle Innenwinkel sind gleich 60°.
• Die Höhe = Mittelsenkrechte = Winkelhalbierende
• Länge der Höhe $h=\frac{a}{2}\sqrt{3}$
• Fläche $A=\frac{ah}{2}=\frac{a^2\sqrt{3}}{4}$
• Umfang $U=3a$

gleichschenkliges Dreieck

Für ein gleichschenkliges Dreieck der Schenkellänge a und der Länge b der dritten Seite gilt:

• Fläche: $A=\frac{1}{2}\cdot b\cdot h=\frac{1}{2}\cdot b\cdot \sqrt{a^2-\frac{b^2}{4}}$
• Umfang: $U=2a+b$
  • Die Höhe auf b ist gleichzeitig die Seitenhalbierende von b.
  • Man kann h also mit dem Pythagoras berechnen:
  • $a^2=h^2+{\left(\frac{b}{2}\right)}^2$
  • $h=\sqrt{a^2-\frac{b^2}{4}}$

Ist der Winkel $\alpha$ zwischen den Schenkeln und die Höhe h bekannt, gilt:

• $b=2h\tan \frac{\alpha }{2}$
• $a=\frac{h}{\cos \frac{\alpha }{2}}$
• $b=2a\sin \frac{\alpha }{2}$

Für ein rechtwinkliges Dreieck mit den Seitenlängen a,b,c gilt

• $a^2+b^2=c^2$
• Dabei liegt die Seite c dem rechten Winkel gegenüber.
• Fläche $A=\frac{ab}{2}$

Für ein beliebiges Dreieck der Seitenlängen a,b,c , den Ecken A,B,C und dem Schwerpunkt S gilt:

$\frac{\overline{CS}}{\overline{SM}}=2:1$ Verhältnis 2 zu 1

Dabei ist:

• C die Ecke C
• S der Schwerpunkt = Schnittpunkt der Seitenhalbierenden
• M der Mittelpunkt der Seite c

Höhenverhältnis:

$h_a:h_b:h_c=\frac{1}{a}:\frac{1}{b}:\frac{1}{c}$

Winkelhalbierende:

$\frac{\overline{AW}}{\overline{WB}}=\frac{b}{a}$

Dabei ist W der Schnittpunkt der Winkelhalbierenden des Innenwinkels der Ecke C ( Winkel ACB) mit der Seite c.

---

Vierecke

Quadrat

Quadrat mit In- und Umkreis

Fläche: $A=a^2$

Umfang: $U=4a$

Länge der Diagonalen: $d=a\sqrt{2}$

Umkreisradius: $r=\frac{a}{2}\sqrt{2}$

Inkreisradius: $r=\frac{a}{2}$

---

Rechteck

Rechteck mit Umkreis

Fläche:

$A=a\cdot b$

Umfang:

$U=2\cdot (a+b)$

Länge der Diagonalen:

$d=\sqrt{a^2+b^2}$

Umkreisradius:

$r=\frac{1}{2}\cdot \sqrt{a^2+b^2}$

Sätze:

• Gegenüberliegende Seiten sind gleich lang und parallel.
• Die beiden Raumdiagonalen sind gleich lang und halbieren einander.
• Der Schnittpunkt der Diagonalen ist Mittelpunkt des Umkreises. Aus diesem Grund ist jedes Rechteck auch ein Sehnenviereck.
• Es ist achsensymmetrisch bezüglich der Mittelsenkrechten (Seitensymmetralen) der Rechteckseiten. Die beiden Symmetrieachsen stehen also senkrecht aufeinander.
• Es ist punktsymmetrisch (zweizählig symmetrisch) bezüglich des Diagonalenschnittpunkts.
• Es ist konvex.

---

Raute (Rhombus)

Fläche:

$A=a\cdot a\cdot \sin \alpha =a\cdot a\cdot \sin \beta \iff F=a^2\cdot \sin \alpha =a^2\cdot \sin \beta$

Umfang: $U=4\cdot a$

Diagonale 1

$e=2\cdot a\cdot \cos \frac{\alpha }{2}=2\cdot a\cdot \sin \frac{\beta }{2}$

Diagonale 2

$f=2\cdot a\cdot \sin \frac{\alpha }{2}=2\cdot a\cdot \cos \frac{\beta }{2}$

Sätze:

• Benachbarte Innenwinkel ergeben als Summe 180 Grad. Alpha + Beta = 180°

---

Parallelogramm

Datei:Parallelogramm-Geom.png

Grundlegende Begriffe am Parallelogramm

Fläche:

$A=a\cdot h_a=b\cdot h_b=a\cdot b\cdot \sin \alpha$

Umfang:

$U=2\cdot (a+b)$

Diagonale e: e²=ha²+(a+x)²
Diagonale 2:
Strecke x: x²=b²-ha²
Sätze:

• Gegenüberliegende Seiten sind gleich lang.
• Gegenüberliegende Winkel sind gleich groß.
• Je zwei benachbarte Winkel sind supplementär (ergeben zusammen 180°).
• Die Diagonalen halbieren sich gegenseitig.
• Jede Diagonale teilt es in zwei (gleich orientierte) kongruente Dreiecke.

---

Trapez

gleichschenkliges Trapez

Fläche:

$A=\frac{1}{2}\cdot (a+c)\cdot h$

Umfang:

$U=a+c+2\cdot b$

Sätze:

• Die Schenkel sind gleich lang. $b=d$

---

ungleichschenkliges Trapez

Trapez

Fläche:

$A=\frac{1}{2}\cdot (a+c)\cdot h$

Umfang:

$U=a+b+c+d$

Diagonale 1

$d_1=\sqrt{a^2+b^2-2ab\cos \beta }=\sqrt{c^2+d^2-2cd\cos \delta }$

Diagonale 2

$d_2=\sqrt{a^2+d^2-2ad\cos \alpha }=\sqrt{b^2+c^2-2bc\cos \gamma }$

---

---

Drachenviereck

Drachenviereck

Sätze über das Drachenviereck:

1. Das Drachenviereck besteht aus zwei gleichschenkligen Dreiecken mit gemeinsamer Basis.
2. Das Drachenviereck ist in sich einfach achsensymmetrisch; die Symmetrieachse ist die durch die Spitzen der gleichschenkligen Teildreiecke verlaufende Diagonale.
3. Das Drachenviereck ist nicht zentralsymmetrisch.
4. Die Diagonalen im Drachenviereck stehen aufeinander senkrecht $e\perp f$.
5. Die Diagonalen im Drachenviereck sind ungleich lang $e=f$.
6. Im Drachenviereck ist ein Gegenwinkel-Paar gleich groß: $\beta =\delta$.
7. Im Drachenviereck werden die ungleich großen Gegenwinkel durch die Diagonale halbiert.

n-Eck

Sätze über das allgemeine n-Eck

1. Die Summe der Innenwinkel eines n-Ecks beträgt $(n-2)\cdot 180^{\circ }$.
2. Die Summe der Außenwinkel eines n-Ecks beträgt $(n+2)\cdot 180^{\circ }$.
3. Ein Innenwinkel und sein zugehöriger Außenwinkel betragen als Nebenwinkel zusammen $180^{\circ }$.
4. Die Winkelhalbierende eines Innenwinkels und die des zugehörigen Außenwinkels stehen senkrecht aufeinander.

Sätze über das regelmäßige n-Eck

1. Jedes regelmäßige n-Eck ist n-fach zentralsymmetrisch.
2. Um jedes regelmäßige Vieleck lässt sich ein Kreis beschreiben, der durch alle Ecken geht. (Umkreis)
3. In jedes regelmäßige Vieleck lässt sich ein Kreis beschreiben, der jede Seite in der Seitenmitte von innen berührt. (Inkreis)
4. Das gemeinsame Zentrum von Um- und Inkreis heißt der Mittelpunkt M des Vielecks.
5. Durch Verbinden des Mittelpunktes mit den Ecken wird das regelmäßige Vieleck in n kongruente gleichschenklige Dreiecke zerlegt.(Bestimmungsdreiecke des Vielecks)
6. Jeder Innenwinkel im regelmäßigen n-Eck beträgt $\frac{n-2}{n}\cdot 180^{\circ }$.
7. Jeder Außenwinkel im regelmäßigen n-Eck beträgt $\frac{360^{\circ }}{n}$

---

Kreis

Grundlegende Begriffe

Grundlegende Begriffe am Kreis

Kreiszahl: $\pi$ = Pi = 3,141592653589793238462643383279...(irrational)

Radius = $r$

Durchmesser = $d$

Kreisbogen = $b$

Durchmesser eines Kreises:

$d=2\cdot r$

Fläche eines Kreises:

$A=r^2\cdot \pi$

Umfang eines Kreises:

$U=d\cdot \pi =2\cdot r\cdot \pi$

Flächeninhalt eines Kreisrings:

$A=(r_1^2-r_2^2)\cdot \pi$

Länge eines Kreisbogens:

$b=\frac{\alpha }{360^{\circ }}\cdot d\cdot \pi$

$b=\frac{\alpha }{180^{\circ }}\cdot r\cdot \pi$

Flächeninhalt von Kreissektoren:

$A_S=\frac{\alpha }{360^{\circ }}\cdot r^2\cdot \pi$

$A_S=\frac{\alpha }{180^{\circ }}\cdot \frac{d^2}{4}\cdot \pi$

$A_S=\frac{1}{2}\cdot b\cdot r=\frac{1}{4}\cdot b\cdot d$

Flächeninhalt eines Kreissegments:

$A=\frac{r^2\cdot \pi \cdot \alpha }{360^{\circ }}-\frac{r^2\cdot \sin \alpha }{2}$

$A=\frac{r^2}{2}\cdot (\frac{\pi \cdot \alpha }{180^{\circ }}-\sin \alpha )$

---

Stereometrie

Kugel

Kugel mit dem Radius r:
Oberfläche: $O=4\pi r^2$

Volumen: $V=\frac{4}{3}\pi r^3$

Siehe auch Wikipedia: Kugel

---

Würfel

Für einen Würfel mit der Seitenlänge a gilt:

• Oberfläche: $O=6a^2$
• Volumen: $V=a^3$
• Länge der Raumdiagonalen: $d=\sqrt{3a^2}$

---

Quader

Skizze eines Quaders

Für einen Quader mit den Seitenlängen a, b, c gilt:

Oberfläche: $O=2(ab+ac+bc)$

Volumen: $V=abc$

Länge der Flächendiagonalen:

$d_1=\sqrt{a^2+b^2}$

$d_2=\sqrt{b^2+c^2}$

$d_3=\sqrt{c^2+a^2}$

Länge der Raumdiagonalen:

$D=\sqrt{a^2+b^2+c^2}$

---

quadratische Pyramide

Für eine Pyramide der Höhe h mit der quadratischen Grundfläche der Seitenlänge a gilt:

Mantelfläche einer quadratischen Pyramide:

$\begin{array}{cc}{A}_M& =4\cdot \mathrm{S}\mathrm{e}\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{f}\mathrm{l}\ddot{\mathrm{a}}\mathrm{c}\mathrm{h}\mathrm{e}\\ & =4\cdot \frac{1}{2}\cdot \mathrm{S}\mathrm{e}\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{l}\ddot{\mathrm{a}}\mathrm{n}\mathrm{g}\mathrm{e}\cdot \mathrm{H}\ddot{\mathrm{o}}\mathrm{h}\mathrm{e}\text{der Pyramidenseite}\\ & =2a\cdot \sqrt{\frac{1}{4}{a}^2+h^2}\end{array}$

Oberfläche einer quadratischen Pyramide:

$\begin{array}{cc}{A}_O& =\mathrm{G}\mathrm{r}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{f}\mathrm{l}\ddot{\mathrm{a}}\mathrm{c}\mathrm{h}\mathrm{e}+4\cdot \mathrm{S}\mathrm{e}\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{f}\mathrm{l}\ddot{\mathrm{a}}\mathrm{c}\mathrm{h}\mathrm{e}\\ & =a^2+2a\cdot \sqrt{\frac{1}{4}{a}^2+h^2}\\ & =a(a+2\cdot \sqrt{\frac{1}{4}{a}^2+h^2})\end{array}$

Volumen einer quadratischen Pyramide:

$\begin{array}{cc}V& =\frac{1}{3}\cdot \mathrm{H}\ddot{\mathrm{o}}\mathrm{h}\mathrm{e}\cdot \mathrm{G}\mathrm{r}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{f}\mathrm{l}\ddot{\mathrm{a}}\mathrm{c}\mathrm{h}\mathrm{e}\\ & =\frac{1}{3}\cdot h\cdot a^2\end{array}$

---

Tetraeder

Für einen Tetraeder mit der Seitenlänge a gilt:

Grundfläche eines Tetraeders:

$A_G=\frac{a^2}{4}\sqrt{3}$

Mantelfläche eines Tetraeders:

$A_M=\frac{3a^2}{4}\sqrt{3}$

Oberfläche eines Tetraeders:

$A_O=a^2\sqrt{3}$

Volumen eines Tetraeders:

$V=\frac{a^3}{12}\sqrt{2}$

Höhe eines gleichseitigen Tetraeders:

$h=\frac{a}{3}\sqrt{6}$

Pyramide, allgemein

Für eine Pyramide der Höhe h mit der Grundfläche A_G und der Mantelfläche A_M gilt allgemein:

Oberfläche einer Pyramide:

$A_O=A_G+A_M$

Volumen einer Pyramide:

$V=\frac{1}{3}{A}_{G}h$

Kreiszylinder

Für einen Kreiszylinder mit der Höhe h und dem Radius r gilt:

Mantelfläche eines geraden Kreiszylinders:

$A_M=\text{Umfang}\cdot h=2\pi rh$

Oberfläche eines geraden Kreiszylinders:

$A_O=A_M+2r^2\pi =2\pi rh+2\pi r^2=2\pi r(h+r)$

Volumen eines geraden Kreiszylinders:

$V=h{r}^2\pi$

---

Kreiskegel

Für einen Kreiskegel der Höhe h mit dem Radius r bzw. dem Durchmesser d und der Mantellinie s gilt:

Mantelfläche eines geraden Kreiskegels

$\begin{array}{cc}{A}_M& =\frac{1}{2}\cdot \pi \cdot d\cdot s\\ & =\pi \cdot r\cdot s\end{array}$

Oberfläche eines geraden Kreiskegels

$\begin{array}{cc}{A}_O& =\frac{1}{4}\cdot \pi \cdot d\cdot (d+2\cdot s)\\ & =\pi \cdot r\cdot (r+s)\end{array}$

Volumen eines geraden Kreiskegels

$\begin{array}{cc}V& =\frac{1}{3}\cdot \mathrm{G}\mathrm{r}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{f}\mathrm{l}\ddot{\mathrm{a}}\mathrm{c}\mathrm{h}\mathrm{e}\cdot \mathrm{H}\ddot{\mathrm{o}}\mathrm{h}\mathrm{e}\\ & =\frac{1}{3}\cdot \pi \cdot r^2\cdot h\\ & =\frac{1}{12}\cdot \pi \cdot d^2\cdot h\end{array}$

Kegelstumpf

Ein gerader Kegelstumpf ist ein parallel zur Grundfläche abgeschnittener Kegel

Mantelfläche eines geraden Kegelstumpfs

$A_M=\pi \cdot s\cdot (r_1+r_2)$

Oberfläche eines geraden Kegelstumpfs

$\begin{array}{cc}{A}_O& =\pi \cdot r_1^2+\pi \cdot r_2^2+A_M\\ & =\pi \cdot r_1^2+\pi \cdot r_2^2+\pi \cdot s\cdot (r_1+r_2)\end{array}$

Volumen eines geraden Kegelstumpfs

$V=\frac{1}{3}\cdot \pi \cdot h\cdot (r_1^2+r_1\cdot r_2+r_2^2)$

---