Mathe für Nicht-Freaks: Gleichmäßige Stetigkeit

{{#invoke:Mathe für Nicht-Freaks/Seite|oben}}

Die gleichmäßige Stetigkeit ist eine stärkere Form der Stetigkeit. Sie leitet sich aus dem Epsilon-Delta-Kriterium der Stetigkeit ab und spielt insbesondere bei der Approximation von Funktionen eine wichtige Rolle.

Motivation

Wiederholung: Epsilon-Delta-Kriterium

Die gleichmäßige Stetigkeit baut auf dem Epsilon-Delta-Kriterium der Stetigkeit auf, weshalb wir dieses zunächst wiederholen:

In jeden noch so kleinen Epsilon-Schlauch um $f(x_0)$ liegen alle Funktionswerte einer hinreichend kleinen Umgebung um $x_0$. Ein Epsilon-Schlauch ist ein Bereich $f(x_0)-ϵ$ bis $f(x_0)+ϵ$ mit $ϵ>0$ um $f(x_0)$:

Eine Funktion f mit einem Epsilon-Schlauch um f(x_0)

Eine Funktion $f:D\to ℝ$ ist genau dann an der Stelle $x_0\in D$ stetig, wenn es für jeden noch so kleinen Epsilon-Schlauch ein $\delta >0$ gibt, so dass alle Funktionswerte von $f$ im Bereich von $x_0-\delta$ bis $x_0+\delta$ in diesen Epsilon-Schlauch liegen:

Alle Funktionswerte von x_0-delta bis x_0+delta liegen im Epsilon-Schlauch um x_0

Dieses $\delta$ kann dabei sowohl von der vorgegebenen Funktion $f$, dem Wert $ϵ$, als auch von der betrachteten Stelle $x_0$ abhängen. Die nächste Grafik zeigt ein Beispiel, bei dem der gefundene $\delta$-Wert zwar für $x_0$ klein genug, für $x_1$ jedoch zu groß ist:

Der Wert für delta ist klein genug für x_0, jedoch zu groß für x_1.

Daher müssen wir das $\delta$ nahe dem Punkt $x_1$ kleiner wählen und bezeichnen die $\delta$-Werte an den Punkten $x_0$ und $x_1$ entsprechend mit ${\delta }_0$ und ${\delta }_1$. Wir sehen, dass das $\delta$ in der Definition der Stetigkeit von der betrachteten Stelle $x$ abhängen kann. Dies ist in nachfolgender Grafik illustriert:

Beide Intervallgrößen delta_1 und delta_2 sind genügend klein für das gegebene psilon gewählt.

Herleitung der gleichmäßigen Stetigkeit

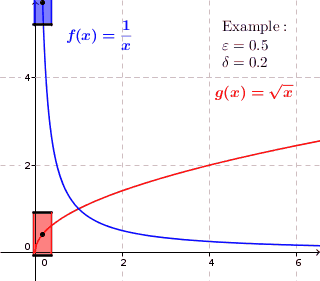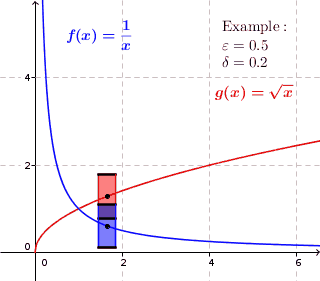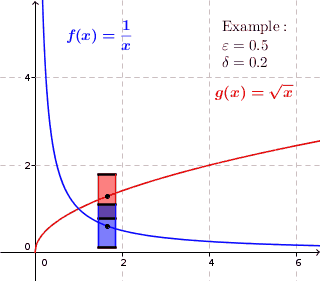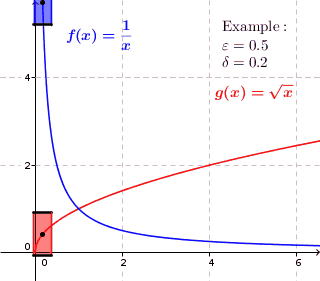
Das Epsilon-Delta-Kriterium garantiert uns so die Approximierbarkeit einer stetigen Funktion $f:D\to ℝ$. Für jeden Maximalfehler $ϵ>0$ und jede betrachtete Stützstelle $\tilde{x}$ finden wir ein ${\delta }_{\tilde{x}}>0$, so dass sich der Funktionswert $f(x)$ für jedes Argument $x$ im Deltabereich $(\tilde{x}-\delta ,\tilde{x}+\delta )$ von $f(\tilde{x})$ um maximal $ϵ>0$ unterscheidet. Für jedes Argument $x$ mit $\tilde{x}-\delta <x<\tilde{x}+\delta$ kann $f(\tilde{x})$ als Annäherung von $f(x)$ mit einem maximalen Fehler von $ϵ$ verwendet werden. Folgende Abbildung illustriert dies für einige eingezeichnete Stellen $x_i$:

Approximation einer stetigen Funktion an verschiedene Stellen.

Jedoch hängen die gefundenen ${\delta }_{\tilde{x}}$-Werte von der betrachteten Stelle $\tilde{x}$ ab. Deswegen sind die Rechtecke in der obigen Grafik auch unterschiedlich groß. Um eine gleichmäßigere Approximation zu erhalten, können wir zusätzlich fordern, dass alle Rechtecke in der Approximation gleich groß sein sollen. D.h. der ${\delta }_{\tilde{x}}$-Wert soll für jedes $\tilde{x}$ gleich sein. Obige Abbildung sähe dann wie folgt aus:

Gleichmäßige Approximation einer stetigen Funktion.

Dies ist die Kernidee der gleichmäßigen Stetigkeit. Bei ihr findet man für ein vorgegebenes $ϵ>0$ ein globales $\delta >0$, so dass egal welche Stelle $\tilde{x}\in D$ man betrachtet, jeder Funktionswert $f(x)$ aus dem Delta-Bereich $(\tilde{x}-\delta ,\tilde{x}+\delta )$ einen Abstand kleiner als $ϵ$ von $f(\tilde{x})$ besitzt. Damit erhalten wir folgende Definition der gleichmäßigen Stetigkeit einer Funktion $f:D\to ℝ$, welche eine gleichmäßige Approximierbarkeit ermöglicht:

Definition

Definition der gleichmäßigen Stetigkeit

Damit können wir die formale Definition der gleichmäßigen Stetigkeit wie folgt aufschreiben:

Anders formuliert heißt dies, dass es zu jedem $ϵ>0$ ein $\delta >0$ gibt, so dass alle Paare $x,\tilde{x}\in D$ mit $|x-\tilde{x}|<\delta$ die Ungleichung $|f(x)-f(\tilde{x})|<ϵ$ erfüllen.

Quantorenschreibweise

Die kommentierte Variante der Quantorenschreibweise lautet:

Vergleicht man die Epsilon-Delta-Definition der gleichmäßigen und der normalen Stetigkeit in Quantorenschreibweise, so fällt auf, dass zwei Quantoren vertauscht sind:

Das beruht darauf, dass bei der gleichmäßigen Stetigkeit das gefundene $\delta$ ein globales Delta ist, welches unabhängig von der Stelle $\tilde{x}\in D$ ist. Um diese Unabhängigkeit auszudrücken, muss der Existenzquantor „$\mathrm{\exists }\delta >0$“ vor dem Allquantor „$\mathrm{\forall }\tilde{x}\in D$“ für die Stützstellen erscheinen.

Herleitung der Negation der gleichmäßigen Stetigkeit

Durch schrittweise Negation der Quantorenschreibweise erhalten wir die Definition der nicht gleichmäßigen Stetigkeit:

Also:

Gleichmäßige Stetigkeit ist eine globale Eigenschaft

Die gleichmäßige Stetigkeit ist eine globale Eigenschaft einer Funktion. Dies bedeutet, dass es nur Sinn ergibt, die gleichmäßige Stetigkeit für eine Funktion als Ganzes zu betrachten. Im Gegensatz dazu ist die normale Stetigkeit eine lokale Eigenschaft. Es ist möglich, die Stetigkeit einer Funktion an nur einer Stelle zu betrachten bzw. zu definieren. Bei der gleichmäßigen Stetigkeit ist dies unmöglich.

Diese Tatsache ergibt sich aus der Definition: Bei der gleichmäßigen Stetigkeit finden wir ein globales $\delta >0$, dessen Delta-Bereich um jede Stützstelle für eine ausreichende Approximation sorgt. Für eine einzelne Stelle ergibt es keinen Sinn zu sagen, dass das gefundene Delta eine globale Gültigkeit hat. Man braucht hier nur eines zu finden.

Visualisierung

Wiederholung: Visualisierung beim Epsilon-Delta-Kriterium

Um das Epsilon-Delta-Kriterium zu visualisieren, zeichnen wir um den betrachteten Punkt $(x_0,f(x_0))$ ein Rechteck mit der Höhe $2ϵ$ und der Breite $2\delta$. Um das Epsilon-Delta-Kriterium zu erfüllen, muss der Graph komplett im Inneren, aber nie direkt ober- oder unterhalb des Rechtecks verlaufen:

Das 2Epsilon-2Delta-Rechteck mit erlaubten und unerlaubten Bereich

Nehmen wir als Beispiel die Quadratfunktion und betrachten die Stelle $x_0=1$. Egal wie klein $ϵ$ vorgegeben ist, wir finden stets ein $\delta$, so dass der Graph komplett im Inneren des $2ϵ$-$2\delta$-Rechtecks liegt:

Visualisierung des Epsilon-Delta-Kriteriums anhand der Quadratfunktion

Wenn im Gegenzug die Funktion wie beim Beispiel der Vorzeichenfunktion $\mathrm{sgn}(x)$ unstetig ist, so finden wir ein $ϵ>0$, bei dem der Graph stets Werte direkt ober- oder unterhalb des Rechtecks besitzt – egal wie klein $\delta$ gewählt wird. Bei der Vorzeichenfunktion im Punkt $x_0=0$ ist dies zum Beispiel bei der Wahl $ϵ=\frac{1}{2}$ der Fall:

• 
  Für $ϵ=\frac{1}{2}$ gibt es bei der Vorzeichenfunktion für $\delta =1$ Funktionswerte, die oberhalb bzw. unterhalb des $2ϵ$-$2\delta$-Rechtecks liegen (rot eingezeichnete Punkte).
• 
  Egal wie klein man das $\delta$ wählt, gibt es Punkte im Graphen, die sich oberhalb bzw. unterhalb des $2ϵ$-$2\delta$-Rechtecks befinden.

Visualisierung der gleichmäßigen Stetigkeit

Bei gleichmäßig stetigen Funktionen kann um jeden Punkt des Graphen ein Rechteck mit Höhe $2ϵ$ und Breite $2\delta$ eingezeichnet werden, ohne dass der Graph direkt ober-/unterhalb des Rechtecks liegt. Die Funktion $f(x)=\sqrt{x}$ ist gleichmäßig stetig. Hier verläuft der Graph nur innerhalb des Rechtecks. Bei der Funkion $g(x)=\frac{1}{x}$ ist dies aber nicht der Fall. Bei kleinen Argumenten in der Nähe der Null verändert sich die Funktion so stark, dass, egal welche Breite des Rechtecks man wählt, Funktionswerte direkt ober- bzw. unterhalb des Rechtecks liegen.

Bei der gleichmäßigen Stetigkeit ist das $\delta$ unabhängig von der betrachteten Stelle. Damit muss der Graph komplett im Inneren des Rechtecks verlaufen, egal mit welchen Punkt des Graphen als Mittelpunkt man es betrachtet. Sprich: Für jedes $ϵ>0$ muss es ein $\delta >0$ geben, so dass man das $2ϵ$-$2\delta$-Rechteck beliebig am kompletten Graphen entlang verschieben kann, ohne dass es Funktionswerte direkt ober- bzw. unterhalb des Rechtecks gibt:

Bei einer gleichmäßigen stetigen Funktion liegt kein Punkt direkt ober- bzw. unterhalb des Rechtecks – egal wo man das Rechteck am Graphen ansetzt.

Bei einer nicht gleichmäßig stetigen Funktion ist dies nicht möglich. Nehmen wir als Gegenbeispiel die Quadratfunktion. Für ein beliebiges $ϵ>0$ können wir kein $\delta >0$ setzen, so dass der Graph überall komplett im Inneren des $2ϵ$-$2\delta$-Rechtecks verläuft, egal wo wir dieses Rechteck ansetzen. Zwar kann bei $x$-Werten in der Nähe der Null der Graph im Inneren des Rechtecks liegen, weil sich dort die Quadratfunktion wenig ändert, aber je mehr wir das Rechteck nach rechts verschieben, desto stärker ist der Anstieg der Quadratfunktion. Irgendwann ist dieser so stark, dass Funktionswerte direkt oberhalb bzw. unterhalb des $2ϵ$-$2\delta$-Rechtecks liegen. Damit ist die Quadratfunktion ein Beispiel einer stetigen Funktion, die nicht gleichmäßig stetig ist:

Die Quadratfunktion als Beispiel für eine nicht gleichmägig stetige Funktion

Beweisschema

Beweisschema: Gleichmäßige Stetigkeit

In Quantorenschreibweise lautet die Definition der gleichmäßigen Stetigkeit:

Aus dieser Aussage kann ein Schema zum Beweis der gleichmäßigen Stetigkeit abgeleitet werden:

Beweisschema: Nicht gleichmäßige Stetigkeit

In Prädikatenlogik lautet die Definition einer nicht gleichmäßig stetigen Funktion $f$:

Daraus ergibt sich ein Schema für den Beweis, dass eine Funktion nicht gleichmäßig stetig ist:

Gleichmäßige Stetigkeit als Verschärfung der Stetigkeit

Die gleichmäßige Stetigkeit ist eine Verschärfung der normalen Stetigkeit. Dies bedeutet, dass jede gleichmäßig stetige Funktion auch stetig ist. Die Umkehrung gilt aber nicht. Es gibt stetige Funktionen wie die Quadratfunktion $f:ℝ\to ℝ:x\mapsto x^2$, die nicht gleichmäßig stetig sind. Also:

Die Quadratfunktion ist stetig, aber nicht gleichmäßig stetig

Wie wir gesehen haben, ist jede gleichmäßig stetige Funktion auch stetig. Die Umkehrung dessen gilt jedoch nicht, weshalb wir als Beispiel nochmals die Quadratfunktion betrachten:Vorlage:Einrücken

Wie wir im Abschnitt Visualisierung bereits gesehen haben, können wir für ein beliebiges $ϵ>0$ kein festes $\delta >0$ setzen, so dass der Graph überall komplett im Inneren des $2ϵ$-$2\delta$-Rechtecks verläuft, egal wo wir dieses Rechteck ansetzen. Je weiter wir das Rechteck nach rechts verschieben, desto stärker der Anstieg der Quadratfunktion, so dass Funktionswerte direkt oberhalb bzw. unterhalb des $2ϵ$-$2\delta$-Rechtecks liegen.

Die können wir auch anhand der Epsilon-Delta-Definition der gleichmäßigen Stetigkeit sehen: $\mathrm{\forall }ϵ>0\mathrm{\exists }\delta >0\mathrm{\forall }\tilde{x}\in ℝ\mathrm{\forall }x\in ℝ:|x-\tilde{x}|<\delta ⟹|f(x)-f(\tilde{x})|<ϵ$. Wir wollen die Negation dieser Aussage beweisen und wollen somit zeigen: $\mathrm{\exists }ϵ>0\mathrm{\forall }\delta >0\mathrm{\exists }\tilde{x}\in ℝ\mathrm{\exists }x\in ℝ:|x-\tilde{x}|<\delta$ und $|f(x)-f(\tilde{x})|\ge ϵ$. Betrachten wir $ϵ=1$ und nehmen wir an es gäbe ein $\delta >0$, sodass $|x_1^2-x_0^2|<ϵ$ für alle reellen Zahlen $x_0,x_1\in ℝ$ mit $|x_1-x_0|<\delta$ gälte. Betrachten wir nun ein $x_0(\delta )>0$ welches wir später festlegen werden. Wir nehmen die Zahlen $x_0$ und $x_1:=x_0+\frac{\delta }{2}$. Nun gilt per Konstruktion $|x_1-x_0|=\frac{\delta }{2}<\delta$.

Wir werden nun zeigen, dass $|x_1^2-x_0^2|\ge ϵ$ gilt.

Somit gilt weiter

Wählen wir nun $x_0\ge \frac{1}{\delta }$ so können garantieren, dass $|x_1^2-x_0^2|\ge 1=ϵ$. Somit haben wir gezeigt, dass

nicht gleichmäßig stetig ist.

Baustelle: Beispiel gleichmäßig stetige Funktionen

• Die Identitätsfunktion $f:D\to D$ ist gleichmäßig stetig, weil wenn $|x-y|<\delta$ gilt, können wir $|f(x)-f(y)|=|x-y|<ϵ$ zeigen, wenn wir $\delta =ϵ$ wählen.

• Oben haben wir gesehen, dass die Quadratfunktion $f:ℝ\to ℝ$ auf den reellen Zahlen nicht gleichmäßig stetig ist. Schränken wir hingegen die Funktion auf ein abgeschlossenes Intervall ein, wird diese neue Funktion gleichmäßig stetig. Es gilt also zum Beispiel, dass

Vorlage:Einrücken gleichmäßig stetig ist. Wir zeigen dies wie folgt: Es gilt Vorlage:Einrücken weil $x,y\in [0,1]$ gilt. Damit können wir $\delta :=\frac{ϵ}{2}$ wählen und erhalten, so dass für alle $x,y\in D$ mit $|x-y|<\delta$ die Abschätzung $|f(x)-f(y)|<2|x-y|<2\delta =ϵ$ gilt.

• Die Wurzelfunktion ist gleichmäßig stetig auf ${ℝ}_0^{+}$. Betrachte:

Vorlage:Einrücken Sei $ϵ>0$ beliebig vorgegeben. Dann ist $\delta ={ϵ}^2$ eine geeignete Wahl: Seien $x,y\in [0,\mathrm{\infty }[$ mit $|x-y|<\delta$.

Ohne Einschränkung können wir annehmen, dass $x\le y$. Dann ist auch $\sqrt{x}\le \sqrt{y}$, also folgt $|\sqrt{x}-\sqrt{y}|=\sqrt{y}-\sqrt{x}$.

Wir wollen nun sehen, dass $|f(x)-f(y)|=|\sqrt{x}-\sqrt{y}|=\sqrt{y}-\sqrt{x}<ϵ$ gilt.

Nach Voraussetzung wissen wir, dass $0\le x\le y<x+{ϵ}^2$. Damit bekommen wir:

Insgesamt haben wir also $y<(\sqrt{x}+ϵ{)}^2$. Weil nach Voraussetzung $x,y\ge 0$ und auch $ϵ>0$ gilt, können wir aus dieser Gleichung die Wurzel ziehen und erhalten $\sqrt{y}<\sqrt{x}+ϵ$, also $\sqrt{y}-\sqrt{x}<ϵ$, was wir oben sehen wollten. Damit haben wir bewiesen, dass $f$ gleichmäßig stetig ist.

• Das nächste Beispiel ist nicht gleichmäßig stetig, es handelt sich um die Funktion

Vorlage:Einrücken welche immer schneller gestreckte Sinuswellen in der Nähe von Null darstellt. Angenommen, $f$ wäre gleichmäßig stetig, dann könnten wir ein geeignetes $\delta$ aus der Definition finden. Für $x\to 0$ wird die Frequenz von $f$ jedoch immer schneller, so dass nahe Null immer eine ganze Periode der Sinusfunktion im $\delta$-Ball enthalten ist. Da der Abstand zwischen dem Maximum und dem Minimum einer Sinuswelle gleich $2$ ist, kann die Bedingung $|f(x)-f(y)|<ϵ$ niemals überall erfüllt sein, wenn $ϵ<2$ ist. Dies wird noch einmal im folgenden Bild illustriert:

This image shows, that the topological sine curve is not uniformly continuous. For an environment of fixed width and x going towards 0, at some point a full period will be inside the environment.

Eigenschaften

Wie wir gesehen haben, ist nicht jede stetige Funktion auch gleichmäßig stetig. Dies trifft jedoch zu, wenn wir den Definitionsbereich einer stetigen Funktion auf ein abgeschlossenes, kompaktes Intervall $[a,b]$ einschränken:

{{#invoke:Mathe für Nicht-Freaks/Seite|unten}}