Digitale bildgebende Verfahren: Transformationen

Digitale bildgebende Verfahren/ Navigation

Dieses Kapitel beschäftigt sich mit mathematischen Transformationen bei optischen Abbildungen und deren Digitalisaten.

Helligkeitstransformationen

Die Leuchtdichten, die in einem Bild die Helligkeiten repräsentieren, werden bei der Digitalisierung in Zahlenwerte umgerechnet, mit denen beliebige mathematische Operationen zur Bildbeeinflussung und zur Bildverbesserung durchgeführt werden können.

Gammakorrektur

Um die mittleren Helligkeiten eines digitalen Bildes anzupassen, ohne die minimale Helligkeit (schwarz) und die maximale Helligkeit (weiß) zu ändern, kann eine rechnerische Gammakorrektur durchgeführt werden, um eine Eingangshelligkeit $E$ in eine Ausgangshelligkeit $A$ umzuwandeln. Der Name dieser Korrektur rührt vom Exponenten $\gamma$ der Übertragungsfunktion her:

$A=E^{\gamma }$

mit

$A,E\in ℝ\mid [0,1]$

und

$\gamma \in ℝ\mid (0,\mathrm{\infty })$

Die Werte für die Eingangshelligkeiten $E$ ergeben sich aus den digitalen Zahlenwerten für die Helligkeit $H_d$ folgendermaßen:

$E=\frac{H_d}{H_{\mathrm{m}\mathrm{a}\mathrm{x}}}$

Der reellwertige Exponent $\gamma$ ist hierbei immer positiv. Die Null und die Eins - also der dunkelste und der hellste Helligkeitswert - bleiben nach der Transformation erhalten, die dazwischenliegenden Werte werden entweder alle vergrößert ($\gamma <1$) oder alle verkleinert ($\gamma >1$). Bei $\gamma =1$ behalten alle Helligkeiten ihren Wert (identische Abbildung).

• Helligkeits- und Farbbalken mit verschiedenen Gammakorrekturen
• 
  Gammakorrektur mit $\gamma =0,5$,
  Mitteltöne werden heller dargestellt
• 
  Originalbild mit $\gamma =1,0$
• 
  Gammakorrektur mit $\gamma =2,0$,
  Mitteltöne werden dunkler dargestellt

Die Gammakorrektur kann daher eingesetzt werden, wenn in einem Bild zwar alle Tonwerte vorhanden sind, jedoch die mittleren Tonwerte zu hell oder wie in folgendem Beispiel zu dunkel wirken:

• Aufnahme eines Springbrunnens im Gegenlicht
• 
  Ausschnitt einer Aufnahme im Gegenlicht. Die Tonwerte verteilen sich zwar über alle Helligkeiten, haben aber ihren Schwerpunkt bei geringen Helligkeiten, so dass das Bild sehr dunkel wirkt, obwohl es nicht unterbelichtet ist.
• 
  Die Tonwerte wurden mit der Gammakorrektur (Parameter $\gamma =0,5$) korrigiert. Die hellsten und dunkelsten Bildpunkte bleiben unverändert, die häufigste Helligkeit hat aber einen deutlich höheren Wert, so dass die Details in den dunklen Bereichen besser hervortreten.

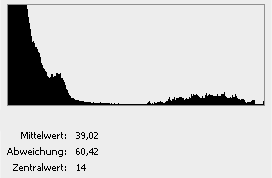
• Histogramme eines Springbrunnens im Gegenlicht
• 
  Histogramm der unkorrigierten dunklen Aufnahme mit $\gamma =1,0$
• 
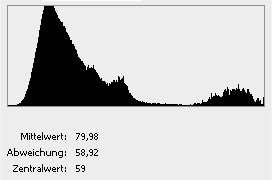
  Histogramm nach der Gammakorrektur mit $\gamma =0,5$

Die Gammakorrektur kann bei Bedarf auch für alle Farbkanäle unabhängig eingestellt werden, wie zum Beispiel bei den drei Primärfarben rot, grün und blau:

$A_r=E_r^{{\gamma }_r}={\left(\frac{H_r}{H_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)}^{{\gamma }_r}$

$A_g=E_g^{{\gamma }_g}={\left(\frac{H_g}{H_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)}^{{\gamma }_g}$

$A_b=E_b^{{\gamma }_b}={\left(\frac{H_b}{H_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)}^{{\gamma }_b}$

Tonwertkorrektur

Weißpunkt

Wenn der Spielraum der ebenfalls Tonwerte genannten Helligkeitswerte in einem digitalen Bild nicht ausgenutzt wird - bei unterbelichteten Bildern ist dies üblicherweise der Fall, da die höheren Helligkeitswerte nicht auftauchen -, ist es sinnvoll, die Helligkeitswerte gleichmäßig zu erhöhen, damit bei der Wiedergabe ein klares Bild mit der Möglichkeit von schwarzen und weißen Bildpunkten entsteht. Die Ausgangswerte $A$ ergeben sich dann auf einfache Weise aus den Eingangswerten $E$ durch eine lineare Transformation:

$A=c\cdot E$

mit

$c=\frac{H_{\mathrm{m}\mathrm{a}\mathrm{x}}}{E_{\mathrm{m}\mathrm{a}\mathrm{x}}}$,

wobei $E_{\mathrm{m}\mathrm{a}\mathrm{x}}$ die maximale im Eingangsbild auftretende Helligkeit ist. Im Ausgangsbild ist nach der Transformation die maximal auftretende Helligkeit gleich 1. Entsprechende Punkte werden auch als die Weißpunkte des Bildes bezeichnet.

• Unterbelichtete Aufnahme einer Kuppel
• 
  Ausschnitt einer unterbelichteten Aufnahme im Gegenlicht, bei der die helle Bildpartie (das Fenster unterhalb des Ausschnittes) weggeschnitten wurde. Die Tonwerte verteilen sich ausschließlich über niedrige Werte.
• 
  Die Tonwerte wurden korrigiert, indem alle Tonwerte ungefähr verdoppelt wurden.

• Histogramme der unterbelichteten Aufnahme einer Kuppel
• 
  Histogramm der unterbelichteten Aufnahme
• 
  Histogramm der korrigierten Aufnahme

Weißabgleich

Eine Tonwertkorrektur kann auch separat für alle vorhandenen Farbkanäle, meist die Primärfarben rot, grün und blau, durchgeführt werden. Um einen Bildbereich farbneutral, also ohne Farbstich, zu bekommen, müssen die entsprechenden Tonwerte der Farbkanäle auf die gleichen Helligkeiten gerechnet werden - diesen Vorgang bezeichnet man als Weißabgleich. Bei Aufnahmesystemen mit automatischem Weißabgleich wird oft in jedem Farbkanal der hellste Punkt gesucht, und mit deren Tonwerten werden die Korrekturen für die einzelnen Farbkanäle ausgerechnet. Bei den üblicherweise verwendeten Primärfarben ergibt sich dann:

$A=\left(\begin{array}{c}{A}_r\\ A_g\\ A_b\end{array}\right)=c\cdot E=c\cdot \left(\begin{array}{c}{E}_r\\ E_g\\ E_b\end{array}\right)=\left(\begin{array}{c}{c}_r\cdot E_r\\ c_g\cdot E_g\\ c_b\cdot E_b\end{array}\right)$

mit

$c=\left(\begin{array}{ccc}{c}_r& c_g& c_b\end{array}\right)=\left(\begin{array}{ccc}\frac{H_{\mathrm{m}\mathrm{a}\mathrm{x}}}{E_{r,\mathrm{m}\mathrm{a}\mathrm{x}}}& \frac{H_{\mathrm{m}\mathrm{a}\mathrm{x}}}{E_{g,\mathrm{m}\mathrm{a}\mathrm{x}}}& \frac{H_{\mathrm{m}\mathrm{a}\mathrm{x}}}{E_{b,\mathrm{m}\mathrm{a}\mathrm{x}}}\end{array}\right)$

wobei $E_{r,\mathrm{m}\mathrm{a}\mathrm{x}}$, $E_{g,\mathrm{m}\mathrm{a}\mathrm{x}}$ und $E_{b,\mathrm{m}\mathrm{a}\mathrm{x}}$ die maximalen im Eingangsbild auftretenden Helligkeiten der drei Farbkanäle sind. Im Ausgangsbild ist nach der Transformation die maximal auftretende Helligkeit für alle Farbkanäle gleich 1. Punkte mit diesen Tonwerten werden auch hier als Weißpunkte bezeichnet.

Problematisch ist der automatische Weißabgleich, wenn es im Eingangsbild gar keine Punkte gibt, die dem Weißpunkt entsprechen. Solche Umstände liegen vor, wenn das aufgenommene Objekt keine weißen Punkte enthält oder monochromatische Punkte die hellsten im Bild sind. Eine typische Situation sind Sonnenauf- und -untergänge, bei der das helle Sonnenlicht eine deutliche Rotfärbung der Szenerie verursacht. Hier ist es in der Regel vorzuziehen, die Farbkanäle nicht für den hellsten Punkt, sondern für einen farbneutralen Punkt (Graupunkt) anzugleichen.

• Mit einer Digitalkamera aufgenommene Schneelandschaft
• 
  Mit automatischem Weißabgleich: der Schnee im Schatten erscheint blau, der Schnee im Hintergrund im Licht der Morgensonne erscheint weiß.
• 
  Mit korrigiertem Weißabgleich: der Schnee im Schatten ist farbneutral (hellgrau), der Schnee im Hintergrund im Licht der Morgensonne ist rötlich und gelblich.

• Histogramme der mit einer Digitalkamera aufgenommenen Schneelandschaft
• 
  Histogramm der Aufnahme mit automatischem Weißabgleich. Blau ist die dominante Farbe.
• 
  Histogramm der Aufnahme mit korrigiertem Weißabgleich. Die Verteilungen der Farben blau und rot wurden durch eine Tonwertkorrektur der Verteilung der Farbe grün angeglichen, so dass alle entsprechenden Bildpunkte farbneutral dargestellt werden.

Koordinatentransformationen

Bildkoordinaten

Zu Bildtransformationen mit den Bildkoordinaten $x$ und $y$, der Bildhöhe $h$ und dem Winkel $\gamma$ zwischen optischer Achse und Bildpunkt bei Abbildungen über eine Hauptebene H in einer Projektionsebene P im Abstand der Bildweite $b$.

Werden die Bildkoordinaten $x$ und $y$ eines Bildpunktes von der Bildmitte aus bestimmt, die in der Regel senkrecht von der optischen Achse durchlaufen wird, ergibt sich der entsprechende Ortsvektor $X$ zu:

$\overrightarrow{X}=\left[\begin{array}{c}x\\ y\end{array}\right]$

Die Bildhöhe $h$ dieses Bildpunktes von der optischen Achse aus gemessen beträgt dann:

$h=\sqrt{x^2+y^2}$

Der Winkel $\gamma$ zwischen optischer Achse und dem Strahl durch den Bildpunkt im Hauptpunkt ist üblicherweise nicht unmittelbar bekannt, kann aber leicht aus der Bildweite $b$ und der Bildhöhe $h$ bestimmt werden:

$\gamma =\arctan \frac{h}{b}$

In der Informationstechnik (IT) wird aus historischen Gründen der Ursprung des Bildkoordinatensystems häufig in die linke obere Bildecke gelegt, wobei die x-Achse nach rechts und die y-Achse nach unten verlaufen. Wenn die Bildbreite $B$ und die Bildhöhe $H$ betragen, ergibt sich die folgende Transformation zu den oben angegebenen Bildkoordinaten:

${\overrightarrow{X}}_{IT}=\left[\begin{array}{c}\frac{B}{2}+x\\ \frac{H}{2}-y\end{array}\right]$

Himmelskoordinaten

Zur Umrechnung: Horizontalsystem ↔ Äquatorialsystem (ruhend).

Der Zenit ist senkrecht über dem Beobachter und der Nadir senkrecht unter dem Beobachter im Zentrum der Darstellung (dunkelgraue Kreisscheibe).

Der Meridian ist der Großkreis durch Himmelsnord- und Himmelsüdpol sowie die Richtungen Norden (N) und Süden (S) vom Beobachter aus gesehen.

Der Beobachter sieht im Horizontalsystem (hellgraue Scheibe) am Himmel einen Punkt (violett) unter dem Azimut $a$ (schwarz), der vom nördlichen Meridian aus im Uhrzeigersinn in der Horizontalebene gemessen wird, und unter dem Höhenwinkel $h$ (grün), der auf dem Großkreis zwischen Nadir und Zenit (grün), der durch den beobachteten Punkt (violett) geht, und der senkrecht zur Horizontalebene und von der Horizontalebene aus gemessen wird.

Diese Winkel können in die kartesischen Koordinaten $x$, $y$ und $z$ im Horizontalsystem umgerechnet werden:

$x=\cos h\cdot \cos a$

$y=\cos h\cdot \sin a$

$z=\sin h$

Diese Koordinaten des entsprechenden Ortsvektors $\overrightarrow{P}$ vom Mittelpunkt in Richtung des beobachteten Punktes sind normalisiert:

$|\overrightarrow{P}|=\left|\left[\begin{array}{c}x\\ y\\ z\end{array}\right]\right|=1$

Im Äquatorialsystem (türkisfarbene Scheibe) wird der Stundenwinkel $\tau$ (cyan) vom nördlichen Meridian aus im Uhrzeigersinn in der Äquatorialebene gemessen, und der Deklinationswinkel $\delta$ (rot) wird auf dem Großkreis zwischen Himmelssüdpol und Himmelsnordpol (rot), der durch den beobachteten Punkt (violett) geht, senkrecht zur Äquatorialebene und von der Äquatorialebene aus gemessen.

Ostpunkt (O) und Westpunkt (W) sind in beiden Systemen identisch, und die Neigung der beiden Ebenen zueinander ist durch die Polhöhe $\varphi$ (blau) gegeben, die mit dem Breitengrad übereinstimmt, auf dem sich der Beobachter befindet.

Für die Umrechnung von Azimut $a$ und Höhenwinkel $h$ im Horizontalsystem in den Stundenwinkel $\tau$ und die Rektaszension im Äquatorialsystem gelten die folgenden Beziehungen:

$\tan \tau =\frac{\sin a}{\sin \varphi \cdot \cos a+\cos \varphi \cdot \tan h}$

und

$\sin \delta =\sin \varphi \cdot \sin h-\cos \varphi \cdot \cos h\cdot \cos a$

Falls der Deklinationswinkel $\delta$, die Sternzeit $\theta$ und die Rektaszension $\alpha$ eines Himmelsobjekts im Äquatorialsystem zum Beispiel mit Hilfe von Ephemeriden-Tabellen bekannt sind, können der der dazugehörige Stundenwinkel $\tau$ und schließlich der entsprechende Azimut $a$ und Höhenwinkel $h$ im Horizontalsystem mit den folgenden Gleichungen berechnet werden:

$\tau =\theta -\alpha$

$\tan a=\frac{\sin \tau }{\sin \varphi \cdot \cos \tau -\cos \varphi \cdot \tan \delta }$

und

$\sin h=\sin \varphi \cdot \sin \delta +\cos \varphi \cdot \cos \delta \cdot \cos \tau$

Scheinbare Bewegung

Der beobachtete Himmelspunkt (violett) bewegt sich in der nördlichen Hemisphäre innerhalb eines halben Tages in Pfeilrichtung auf einem Halbkreis (mit $180^{\circ }$ respektive $\pi \text{rad}$) von Osten nach Westen, der mit konstantem Deklinationswinkel $\delta$ (rot) parallel zur Äquatorialebene (türkisfarbene Scheibe) liegt. Innerhalb eines ganzen siderischen Tages $(1\text{d}\approx 23,9345\text{h}\approx 86164,2\text{s})$ wird ein vollständiger Kreis durchlaufen.

Innerhalb einer vorgegebenen Zeitspanne $\mathrm{\Delta }t$ in Sekunden verändert sich der Stundenwinkel $\tau$ demnach im Bogenmaß um den Betrag:

$\mathrm{\Delta }\tau =\frac{2\pi }{86164,2\text{s}}\cdot \mathrm{\Delta }t=7,2921\cdot 10^{-5}\text{Hz}\cdot \mathrm{\Delta }t$

Der neue Stundenwinkel ${\tau }^{\prime }$ beträgt dann also:

${\tau }^{\prime }=\tau +\mathrm{\Delta }\tau$

Mithilfe des neuen Strundenwikels ${\tau }^{\prime }$ kann dann auch die neue Position des betrachteten Punktes im Horizontalsystem bestimmt werden:

$\tan a^{\prime }=\frac{\sin {\tau }^{\prime }}{\sin \varphi \cdot \cos {\tau }^{\prime }-\cos \varphi \cdot \tan \delta }$

und

$\sin h^{\prime }=\sin \varphi \cdot \sin \delta +\cos \varphi \cdot \cos \delta \cdot \cos {\tau }^{\prime }$

Die scheinbare Bewegung des betrachteten Himmelspunktes kann durch die Differenz der Azimute

$\mathrm{\Delta }a=a^{\prime }-a$

und die Differenz der Höhenwinkel

$\mathrm{\Delta }h=h^{\prime }-h$

ausgedrückt werden.

Beispiel

Das folgende Beispiel für den Blutmond am 28. September 2015 ist für den 52. Breitengrad südlich von Berlin und eine Zeitdifferenz (= Belichtungszeit) von sechs Sekunden berechnet:

Himmelskoordinaten des Blutmonds am 28. September 2015

Winkel	Winkel in Grad	Winkel im Bogenmaß (Radiant)
Polhöhe $\varphi$	52,000	0,90757
Azimut $a$	56,000	0,97738
Höhenwinkel $h$	29,000	0,50615
Deklination $\delta$	4,64184	0,08102
Stundenwinkel $\tau$	46,6754	0,81464
Stundenwinkeldifferenz $\mathrm{\Delta }\tau$	0,0251	0,00044
Neuer Stundenwinkel ${\tau }^{\prime }$	46,7005	0,81508
Neuer Azimut $a^{\prime }$	56,0245	0,97781
Neuer Höhenwinkel $h^{\prime }$	28,9872	0,50592
Azimutdifferenz $\mathrm{\Delta }a$	0,02454	0,00043
Höhenwinkedifferenz $\mathrm{\Delta }h$	-0,01280	-0,00022

Projektion

Zentralprojektion der Punkte P und P' am Himmel auf die Punkte Q und Q' in einer Bildebene in der Entfernung f vom Mittelpunkt der Projektion M.

Im Folgenden wird die Bewegung eines Himmelspunktes von P mit dem Azimut $a$ und dem Höhenwinkel $h$ nach P' mit dem Azimut $a^{\prime }$ und dem Höhenwinkel $h^{\prime }$ betrachtet, der von einem Mittelpunkt M aus in der unbewegten Projektionsebene mit x- und y-Koordinate als Verschiebung von Bildpunkt Q nach Bildpunkt Q' erscheint.

Bei einer Bildweite, die bei einer Abbildung aus dem Unendlichen mit der Brennweite $f$ identisch ist, ergeben sich in der Bildebene, deren horizontale x-Achse parallel zum Horizont ausgerichtet ist und deren Normale (= optische Achse der Abbildung durch den Bildpunkt Q zum Punkt P) auf den betrachteten Punkt P zeigt, die folgenden Koordinatendifferenzen aus den Winkeldifferenzen im Bogenmaß:

$\mathrm{\Delta }x=f\cdot \mathrm{\Delta }a$

$\mathrm{\Delta }y=f\cdot \mathrm{\Delta }h$

Beispiele

Bei Beobachtung am Äquator (${\varphi }_{Equ}=0$) vereinfacht sich die Betrachtung folgendermaßen:

$\mathrm{\Delta }{x}_{Equ}=0$

$\mathrm{\Delta }{y}_{Equ}=f\cdot \mathrm{\Delta }\tau$

Umgekehrt verhält es sich bei der Beobachtung am Nord- oder Südpol (${\varphi }_{Pol}=\pm 90^{\circ }$):

$\mathrm{\Delta }{x}_{Pol}=\pm f\cdot \mathrm{\Delta }\tau$

$\mathrm{\Delta }{y}_{Pol}=0$

Die folgenden Werte sind für eine Brennweite von 140 Millimetern und für die Winkel im oben angegebenen Beispiel berechnet ($\varphi =52^{\circ }$). Die Breite und Höhe eines Bildpunkts entsprechen bei den folgenden Beispielbildern einer Länge von 7,4 Mikrometern in der Bildebene. Der Bildausschnitt auf dem Bildsensor betrug rund 7,6 mal 5,7 Quadratmillimeter.

Bildtranslation des Blutmonds am 28.  September 2015

Verschiebung	Wert
Horizontale Verschiebung in mm	0,060
Vertikale Verschiebung in mm	-0,031
Horizontale Verschiebung in Pixel	8
Vertikale Verschiebung in Pixel	-4

• Blutmond am 28. September 2015 mit verschiedenen Belichtungszeiten
• 
  Mit einer Belichtungszeit von einer Sekunde
  (Belichtungsindex ISO 1600 mit -0,3 Stufen Korrektur des Belichtungswertes).
• 
  Mit einer Belichtungszeit von sechs Sekunden
  (Belichtungsindex ISO 200 ohne Korrektur des Belichtungswertes).

Bilddrehung

Bilddrehung um den Winkel $\gamma$ zwischen den Punkten Q und Q' durch die Drehung der Erde um den Himmelsnordpol mit dem Winkel $\gamma$.

Bei entsprechend langen Belichtungszeiten kann es erforderlich sein, auch die Bilddrehung zu berücksichtigen. Das Bild dreht sich genauso wie die Erde einmal pro (siderischem) Tag.

Der Winkel der Bilddrehung $\gamma$ ist daher identisch mit der Stundenwinkeldifferenz $\mathrm{\Delta }\tau$:

$\gamma =\mathrm{\Delta }\tau$

Am Himmelsäquator ist die Deklination $\delta =0$, und es ergibt sich keine Rotation. In der nördlichen Hemisphäre ($\delta >0$) ist die scheinbare Drehung eines Fixsterns entgegen dem Uhrzeigersinn und in der südlichen Hemisphäre ($\delta <0$) im Uhrzeigersinn.

Beispiel

Das folgende Beispiel ist erneut mit den obigen Vorgaben für eine Brennweite von 140 Millimetern und für eine Zeitdifferenz (= Belichtungszeit) von sechs Sekunden berechnet:

Bildrotation des Blutmonds am 28.  September 2015

Winkel	Wert
Drehwinkel in rad	0,00044
Drehwinkel in °	0,02500
Drehwinkel in '	1,50
Drehwinkel in "	90

Entlang einer Bildkantenlänge von 1024 Bildpunkten mit je 7,4 Mikrometern ergibt sich eine Bilddrehung um knapp einen halben Bildpunkt beziehungsweise eine Verdrehung der Bildecke um 3,3 Mikrometer.

Fourier-Transformation

Programm zur Berechnung einer Fast-Fourier-Transformation in Component Pascal.

Der Betrag der komplexwertigen, zweidimensionalen Fourier-Transformation der Bilddaten im Bildraum kann zur Ermittlung der spektralen Dichte der Modulationsübertragungsfunktion im Ortsfrequenzraum herangezogen werden. In der digitalen Signalverarbeitung wird hierfür häufig die sehr effiziente Fast-Fourier-Transformation (FFT) eingesetzt.

Siehe auch Programm in der Programmiersprache Component Pascal zur Berechnung einer zweidimensionalen Fast-Fourier-Transformation.

Das Leistungsdichtespektrum entspricht hierbei dem Beugungsbild der Bilddaten, das mit einem Bildschirm aufgefangen werden kann.

Beispiele

• Kontrastübertragungsfunktion an Beispielen
• 
  Vertikaler Doppelspalt.
• 
  Das Leistungsdichtespektrum des vertikalen Doppelspalts. Nur die Ortsfrequenzen, die exakt in horizontaler Richtung liegen, tragen zur Kontrastübertragung bei. Die Ortsfrequenz null befindet sich in der Mitte der Beugungsbilder und nimmt radial in alle Richtungen zu.
• 
  Periodisches Liniengitter.
• 
  Das Leistungsdichtespektrum des Liniengitters. Nur die Ortsfrequenzen, die exakt in horizontaler Richtung liegen, tragen zur Kontrastübertragung bei. Durch die Periodizität des Liniengitters werden die Beugungsmaxima respektive die auftretenden Ortsfrequenzen schärfer und haben somit eine geringere Bandbreite.
• 
  Schachbrettmuster.
• 
  Das Leistungsdichtespektrum des Schachbrettmusters. Nur die Ortsfrequenzen, die exakt in horizontaler oder vertikaler Richtung liegen, tragen zur Kontrastübertragung bei. Durch die Periodizität des Schachbrettmusters sind die Beugungsmaxima scharf respektive haben die auftretenden Ortsfrequenzen eine geringe Bandbreite.
• 
  Siemensstern mit einer maximalen Ortsfrequenz von 1024 Linienpaaren pro Bildhöhe (in Originalgröße).
• 
  Leistungsdichtespektrum des Siemenssterns (an den Bildkantenmitten beträgt die Ortsfrequenz 1024 Linienpaare pro Bildhöhe).
• 
  Mit einem Tiefpass gefilterter Siemensstern mit einer maximalen Ortsfrequenz von zirka 330 Linienpaaren pro Bildhöhe - die Kanten sind breiter und wirken somit weicher, die Details in der Bildmitte sind verloren gegangen.
• 
  Leistungsdichtespektrum des mit einem Tiefpass gefilterten Siemenssterns mit einer maximalen Ortsfrequenz von 330 Linienpaaren pro Bildhöhe.

Digitale bildgebende Verfahren/ Navigation