Mathe für Nicht-Freaks: Binomialkoeffizient: Rechenregeln

In diesem Kapitel stelle ich dir die wichtigsten Eigenschaften des Binomialkoeffizienten vor.

Rechenregeln in der Übersicht

Es sei im Folgendem $k$ und $n$ eine natürliche Zahl, wobei $k$ und $n$ hier auch Null sein dürfen. Außerdem sei $0 \leq k \leq n$ . Es gelten nun folgende Regeln:

$(\binom{n}{0}) = 1$
$(\binom{n}{n}) = 1$
$(\binom{n}{k}) = (\binom{n}{n - k})$
$k \cdot (\binom{n}{k}) = n \cdot (\binom{n - 1}{k - 1})$
$(\binom{n + 1}{k + 1}) = (\binom{n}{k}) + (\binom{n}{k + 1})$ für $0 \leq k < n$

Einige der obigen Gleichungen können gut aus der Anschauung des Binomialkoeffizienten erklärt werden, dass $(\binom{n}{k})$ der Anzahl der $k$ -elementigen Teilmengen einer $n$ -elementigen Menge entspricht:

$(\binom{n}{n}) = 1$ weil eine $n$ -elementige Menge $M$ nur eine $n$ -elementige Teilmenge enthält (nämlich die Menge $M$ ).
$(\binom{n}{k}) = (\binom{n}{n - k})$ . Zu jeder Teilmenge von $M$ mit $k$ Elementen existiert deren Komplement, welches $n - k$ Elemente enthält. Somit ist die Anzahl der unterschiedlichen Teilmengen gleich.
$(\binom{n + 1}{k + 1}) = (\binom{n}{k}) + (\binom{n}{k + 1})$ . Stellen wir uns Mengen $M, M^{'} : = M \cup {e}$ vor, wobei $| M | = n$ und $e$ ein zuvor nicht in $M$ enthaltenes Element ist. Dann ist der erste Summand die Anzahl der $k$ -elementigen Teilmengen von $M$ - fügt man aber jeder dieser Mengen das neue Element $e$ hinzu, sind diese nun $k + 1$ -elementige Teilmengen von $M^{'}$ . Zusammen mit den $k + 1$ -elementigen Teilmengen ohne $e$ (der zweite Summand), erhalten wir das Ergebnis.

Andere Rechenregeln sind aber nicht so offensichtlich. Hier kann im Beweis auf die Fakultätsdefinition $(\binom{n}{k}) = \frac{n!}{k! (n - k)!}$ des Binomialkoeffizienten zurückgegriffen werden.

Pascalsches Dreieck

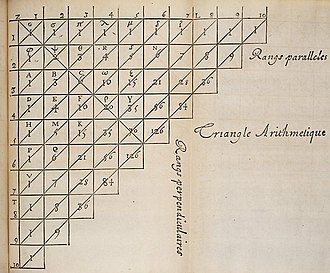
Das pascalsche Dreieck ist eine grafische Anordnung der Binomialkoeffizienten in einem Dreieck:

Vorlage:Einrücken

Wenn man die Binomialkoeffizienten ausrechnet, dann ergibt sich folgendes Dreieck:

Vorlage:Einrücken

Die Regel $(\binom{n + 1}{k + 1}) = (\binom{n}{k}) + (\binom{n}{k + 1})$ ermöglicht es, den Binomialkoeffizienten als Summe der beiden direkt oberhalb liegenden Binomialkoeffizienten zu berechnen:

Animation zur Erstellung des Pascalschem Dreieck

Das Besondere am pascalschen Dreieck ist, dass man an ihm direkt die Binomalkoeffizienten und damit die Vorfaktoren beim Ausklammern von Potenzen der Form $(x + y)^{n}$ ablesen kann. Beispielsweise lautet die Zeile für $n = 3$ :

Vorlage:Einrücken

Dies ist die vierte Zeile, weil die erste Zeile im Dreieck zu $n = 0$ gehört. Damit wissen wir ohne Nachrechnen:

Vorlage:Einrücken

Der Sinn des pascalschen Dreiecks ist es also, die Vorfaktoren beim Ausklammern von Potenzen der Form $(x + y)^{n}$ einfach ablesen zu können. Das Dreieck wurde im Übrigen nach Blaise Pascal benannt, der es 1655 in einem seiner Bücher veröffentlichte. Es wurde aber bereits früher von anderen Mathematikern eingesetzt^[1].

Beweise zu den Rechenregeln

Mathe für Nicht-Freaks: Binomialkoeffizient: Rechenregeln

Inhaltsverzeichnis

Rechenregeln in der Übersicht

Pascalsches Dreieck

Beweise zu den Rechenregeln

Regel 1 und 2 Vorlage:Anker

Regel 3

Regel 4

Regel 5

Navigationsmenü

Mathe für Nicht-Freaks: Binomialkoeffizient: Rechenregeln

Rechenregeln in der Übersicht

Pascalsches Dreieck

Beweise zu den Rechenregeln

Regel 1 und 2 Vorlage:Anker

Regel 3

Regel 4

Regel 5

Navigationsmenü

Suche