Brückenkurs Mathematik/ Hauptteil/ Erster Teil

<< Anfang

Prozentrechnung

Übung:

a) Berechnen sie die reale Preissteigerung eines Produktes, bei dem der Preis um 10% steigt 
   und gleichzeitig der Inhalt um 15% abgenommen hat.

b) Bei einer Wahl gehen 40% der Wahlberechtigten nicht zur Wahl. 10% der gültigen Stimmen 
   entfallen auf Parteien, die an der 5%-Hürde scheitern. Für die siegreiche Partei  
   entscheiden sich 36% aller Wahlberechtigten. Wieviel Prozent der Sitze im Parlament erhält 
   diese Partei?

Dreisatz

Proportional

Ist der Quotient zweier Größen eine Konstante liegt direkte Proportionalität vor.

$\frac{a}{b}=\frac{c}{x}$

Übung:
  
Ergänzen Sie die Proportionen:

a) $\frac{2}{3}=\frac{5}{?}$

b) $\frac{2x}{7y}=\frac{?}{14y^{2}u}$

c) Ein Pkw verbraucht auf 100 km 9,4 Liter Benzin.
   Mit einer Tankfüllung kommt er 540 km weit.
   Wie viel Liter fasst der Tank ?

Antiproportional

Ist das Produkt zweier Größen konstant liegt indirekte Proportionalität vor.

$a\cdot b=c\cdot x$

Übung:
 
a) Drei Pflasterer benötigen für eine Hofeinfahrt 11,5 Stunden.
   Wie lange brauchen 5 Pflasterer?

b) Auf einer Wippe sitzt ein Kind mit 36kg im Abstand von 2m vom Drehpunkt.
   In welchem Abstand muß ein 24kg schweres Kind sitzen, damit die Wippe im 
   Gleichgewicht ist?

Verschachtelt I

Übung:
 
Ein 7 m2 großes Blech, 5 mm dick, wiegt 313,6 kg.
Wie viel wiegt ein 6 mm dickes Kupferblech, das eine Fläche von 4 m2 hat?

Verschachtelt II

Übung:
 
Für 720 m2 Pflaster brauchen 7 Arbeiter 160 h.
Wie lange benötigen 5 Arbeiter für 600 m^2.
(Zeitangabe in Stunden und Minuten)

Verschachtelt III

Übung:

Zwölf Einschaler haben bei 9 - stündiger Arbeitszeit in 7 Tagen 390 m2
Betonschalung    hergestellt.
Wie viel Einschaler sind bei gleicher Leistung einzusetzen, 
wenn in insgesamt 21 Tagen  2340 m2 Betonschalung hergestellt werden müssen,
und die tägliche Arbeitszeit nur 8 Stunden beträgt?

Mittelwerte

Im Folgenden seien $x_1\dots x_n$ gegebene reelle Zahlen, z.B. Messwerte, deren Mittelwert berechnet werden soll.

Arithmetisches Mittel

Es ist so definiert:

${\overline{x}}_{\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{m}}=\frac{x_1+x_2+\cdots +x_n}{n}$

Beispiel:

Ein Auto fährt eine Stunde lang 100 km/h und die darauf folgende Stunde   
200 km/h. Mit welcher konstanten Geschwindigkeit muss ein anderes Auto fahren, um  
denselben Weg ebenfalls in 2 Stunden zurückzulegen?

Der Weg $s_1$, den das erste Auto insgesamt zurückgelegt hat, beträgt
$s_1=100\mathrm{k}\mathrm{m}/\mathrm{h}\cdot 1\mathrm{h}+200\mathrm{k}\mathrm{m}/\mathrm{h}\cdot 1\mathrm{h}.$
und der des zweiten Autos
$s_2=v_2\cdot 2\mathrm{h},$
wobei $v_2$ die Geschwindigkeit des zweiten Autos ist. 
Aus $s_1=s_2$ ergibt sich
$v_2\cdot 2\mathrm{h}=100\mathrm{k}\mathrm{m}/\mathrm{h}\cdot 1\mathrm{h}+200\mathrm{k}\mathrm{m}/\mathrm{h}\cdot 1\mathrm{h}.$
und damit
$v_2=\frac{100\mathrm{k}\mathrm{m}/\mathrm{h}\cdot 1\mathrm{h}+200\mathrm{k}\mathrm{m}/\mathrm{h}\cdot 1\mathrm{h}}{2\mathrm{h}}=\frac{100\mathrm{k}\mathrm{m}+200\mathrm{k}\mathrm{m}}{2\mathrm{h}}=150\mathrm{k}\mathrm{m}/\mathrm{h}.$

Gewichtetes arithmetisches Mittel:

Beispiel:

Das arithmetische Mittel von 5 Zahlen ergibt sich auch als mit den Anzahlen von  
Teilmengen gewichteter Mittelwert der Teilmittelwerte:
$\overline{x}=\frac{1+2+3+4+5}{5}=\frac{3\frac{1+2+3}{3}+2\frac{4+5}{2}}{3+2}=\frac{n_1{\overline{x}}_1+n_2{\overline{x}}_2}{n_1+n_2}=\frac{6+9}{3+2}=3.$

Beispiel:

Berechnung eines Massenmittelpunktes/Schwerpunktes

Übung:

Ein Bauer stellt im Nebenerwerb 100 kg Butter her. 10 kg kann er für 10 
€/kg verkaufen, weitere 10 kg für 6 €/kg und den Rest muss er für 3 €/kg  
verschleudern. Zu welchem (gewichtetem) Durchschnittspreis hat er seine Butter 
verkauft?

Geometrisches Mittel

Definition:

${\overline{x}}_{\mathrm{g}\mathrm{e}\mathrm{o}\mathrm{m}}=\sqrt[n]{x_1\cdot x_2\cdot \dots \cdot x_n}$

Es ist ein geeigneter Mittelwert für Größen, von denen das Produkt von Bedeutung ist, z.B. von Verhältnissen oder Wachstumsraten.

Beispiel:
 
Das Mittel aus einer Verdopplung und nachfolgender Verachtfachung einer  
Bakterienkultur ist eine Vervierfachung (nicht eine Vermehrung um den Faktor 5).

Übung:

Ein Guthaben G wird im ersten Jahr mit zwei Prozent, im zweiten Jahr mit  
sieben und im dritten Jahr mit fünf Prozent verzinst. Welcher über die drei Jahre  
konstante Zinssatz p hätte zum Schluss das gleiche Kapital ergeben?

Harmonisches Mittel

Das harmonische Mittel ist definiert als:

${\overline{x}}_{\mathrm{h}\mathrm{a}\mathrm{r}\mathrm{m}}=\frac{n}{\sum _{i=1}^n\frac{1}{x_i}}.$

Durch Bildung des Kehrwertes erhält man

$\frac{1}{{\overline{x}}_{\mathrm{h}\mathrm{a}\mathrm{r}\mathrm{m}}}=\frac{\sum _{i=1}^n\frac{1}{x_i}}{n}$,

der Kehrwert des harmonischen Mittels ist also das arithmetische Mittel der Kehrwerte.

Beispiel:

harmonisches Mittel von 5 und 20:
$\frac{2}{\frac{1}{5}+\frac{1}{20}}=\frac{2}{\frac{1}{4}}=8$ 

Übung:

Ein Fahrzeug fährt 100 km mit 50 km/h und dann 100 km mit   
100 km/h. Wie groß ist die Durchschnittsgewschindigkeit?

Allgemein gilt: Benötigt man für die Teilstrecke $s_1$ die Zeit $t_1$ (also Durchschnittsgeschwindigkeit $v_1=s_1/t_1$) und für die Teilstrecke $s_2$ die Zeit $t_2$ (also Durchschnittsgeschwindigkeit $v_2=s_2/t_2$, so gilt für die Durchschnittsgeschwindigeit über die gesamte Strecke $v=\frac{s_1+s_2}{t_1+t_2}=\frac{s_1+s_2}{\frac{s_1}{v_1}+\frac{s_2}{v_2}}=\frac{t_1{v}_1+t_2{v}_2}{t_1+t_2}$ Die Durchschnittsgeschwindigkeit ist also das mit den Wegstrecken gewichtete harmonische Mittel der Teilgeschwindigkeiten oder das mit der benötigten Zeit gewichtete arithmetische Mittel der Teilgeschwindigkeiten.

Gemeinsame Definition der klassischen Mittelwerte

Die Idee, die den drei klassischen Mittelwerten zugrunde liegt, lässt sich auf folgende Weise allgemein formulieren:

Beim arithmetischen Mittel sucht man die Zahl m, für die gilt:

$m+m+\dots +m=n\cdot m=x_1+\dots +x_n$,

Beim geometrischen Mittel sucht man die Zahl m, für die gilt:

$m\cdot m\cdot \dots \cdot m=m^n=x_1\cdot \dots \cdot x_n$,

Das harmonische Mittel m löst die Gleichung

$n\cdot \frac{1}{m}=\frac{1}{x_1}+\dots +\frac{1}{x_n}$.

Elementare Rechenregeln

Operationen,Terme,Baumstruktur

• Vorzeichenregeln - Division analog

$(+a)(+b)=(-a)(-b)=+ab$

$(+a)(-b)=(-a)(+b)=-ab$

• Ausklammern, Faktorisieren

$\pm ax\pm bx=\pm x(a+b)$
$\pm ax\mp bx=\pm x(a-b)$

Übung:
Teilweise werden Potenzgesetze vorausgesetzt. Siehe dort!

a) $289xyz+34zyx-17yz+51zx$

b) $12a^3{b}^2-30a^{4}bc+18a^2{b}^3{c}^2$

c) $(a-b)\cdot 2a-(a-b)\cdot 3b+7(a-b)$

d) $(x+y{)}^2-x-y+(2x+2y)\cdot 3x$

e) $3ac-5ad+3bc-5bd$

f) $2a^{2}x-5abx+7b^{2}x-2a^{2}y+5aby-7b^{2}y$

g) $6fk-15fl+3f+2gk-5gl+g-4hk+10hl-2h$

h) $-e^{2x}\cdot (-x^2+3x-7)\cdot (-2)+(x^2-2x+14)\cdot e^x$

• Ausmultiplizieren, Klammern Auflösen

$a+(b+c-d)=a+b+c-d$
$a-(b+c-d)=a-b-c+d$

Übung:


a) $\frac{1}{3}(-5x+3y-\frac{15}{2})(-6)$

b) $-2xy\left(\frac{15}{4}{x}^{2}y\right)(-x+\frac{2}{3}xy-\frac{1}{3}y)$

c) $(5-3a)(125+75a+45a^2+27a^3)$

d) $(2-5x)(3+7x)(10x+4)$ 

e) $(7p-5q+4r)(8r-14p+10q)-4(8r^2+35pq)$

f) $(f^2-\frac{1}{3}{g}^2)(-3e^2)-e(-\frac{3}{2}ef+eg)(2f-g)$

g) $[-3+(-\frac{9}{2}a+5)]\cdot [2a-(3-\frac{1}{2}a)]$

h) $-2x(y-1)-[3x-(1+5x)]\cdot [2y-(2+y)]$

Übung:

a) $\{5x(-3ab)-b(-14ay)+4ab(6z+6x-2y)\}÷(3ab)$

• Operationsbaum

Brüche

• Addition/Subtraktion

$\frac{a}{b}+\frac{c}{d}=\frac{a\cdot d+c\cdot b}{b\cdot d}$

$\frac{a}{n}+\frac{b}{n}=\frac{a+b}{n}$

Anmerkung: Primzahlzerlegung und kgV-Bestimmung

• Multiplikation

$\frac{a}{b}\cdot \frac{c}{d}=\frac{a\cdot c}{b\cdot d}$

$\frac{a}{b}\cdot n=\frac{a}{b}\cdot \frac{n}{1}=\frac{a\cdot n}{b}$

• Division

$\frac{a}{b}:\frac{c}{d}=\frac{a}{b}\cdot \frac{d}{c}=\frac{a\cdot d}{b\cdot c}$

$\frac{a}{b}:n=\frac{a}{b\cdot n}$

• Kürzen und Erweitern

Kürzen: $\frac{Z}{N}=\frac{a\cdot c}{b\cdot c}=\frac{a}{b}$

Ausklammern des Faktors c sowohl aus Zähler als auch aus Nenner. Das ergibt eine "EINS"-Multiplikation, die gekürzt werden kann.

Erweitern: $\frac{a}{b}=\frac{a\cdot c}{b\cdot c}=\frac{Z}{N}$

Der Bruch wird mit "Eins" multipliziert, also Zähler und Nenner jeweils mit demselben Faktor c.

Beispiel:

$\frac{1}{\frac{1}{a}+\frac{1}{b}}=\frac{1}{\frac{b+a}{ab}}=\frac{1\cdot ab}{\frac{b+a}{ab}\cdot ab}=\frac{ab}{b+a}$ 

Übung:

a) $(\frac{3}{4}+\frac{5}{8})÷(\frac{1}{2}+\frac{4}{3})$

b) $\frac{\frac{a^2}{b}+\frac{b^2}{a}}{\frac{1}{a}+\frac{1}{b}}$

 
c) $\frac{\frac{1}{s^2-1}-\frac{1}{s^2}}{2+\frac{1}{s-1}-\frac{1}{s+1}}$
 
 
d) $1-\frac{u}{1-\frac{u}{u+1}}$
 
 
e) $\frac{11a-3}{2x+3}-\frac{7a-4}{2x+2}+\frac{5a-6}{6x+6}$

Potenzen

Das Potenzieren ist eine abkürzende Schreibweise für eine wiederholte Multiplikation. Die Potenz $a^n$ wird definiert durch

$\begin{array}{c}{a}^n:=\underset{n\mathrm{F}\mathrm{a}\mathrm{k}\mathrm{t}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{n}}{\underbrace{a\cdot a\cdot a\cdots a}}\end{array}$

$a$ heißt Basis (oder Grundzahl), $n$ heißt Exponent (oder Hochzahl) der Potenz $a^n$.

Die Potenzschreibweise kann man auch folgendermaßen verstehen: „Multipliziere die Zahl 1 mit so oft mit der Basis, wie der Exponent angibt“:

$\begin{array}{c}{a}^n=1\cdot \underset{n\mathrm{F}\mathrm{a}\mathrm{k}\mathrm{t}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{n}}{\underbrace{a\cdot a\cdot a\cdots a}}\end{array}$

Der Exponent n=0 bedeutet dann, dass gar nicht mit der Basis zu multiplizieren ist, so dass man das Ergebnis 1 erhält.

$a^0:=1$

Negative Exponenten bedeuten, dass man die zur Multiplikation inverse Operation (Division) durchführen soll. Also „Dividiere die Zahl 1 durch die Grundzahl so oft, wie die Hochzahl angibt“.

$\begin{array}{c}{a}^{-n}=1:\underset{n\mathrm{D}\mathrm{i}\mathrm{v}\mathrm{i}\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{n}}{\underbrace{a:a:a:a}}\end{array}$

Für eine reelle Zahl $a$ und eine natürliche Zahl $n$ wird definiert

$a^{-n}:=\frac{1}{a^n},a\ne 0$

Die Rechenregeln:

$a^{r+s}=a^r\cdot a^s$	$a^{r-s}=\frac{a^r}{a^s}$	$(a^r{)}^s=a^{r\cdot s}$	$(a\cdot b{)}^r=a^r\cdot b^r$	${\left(\frac{a}{b}\right)}^r=\frac{a^r}{b^r}$

Beispiel:

${\left(\frac{1}{-3}\right)}^{-3}=\frac{1}{{\left(\frac{1}{-3}\right)}^3}=\frac{1}{\frac{{\left(1\right)}^3}{{(-3)}^3}}=\frac{1}{\frac{1}{-27}}=-27$

Übung:

a) $\frac{9b^3}{25a^{-4}}\cdot \frac{20b^{-4}}{16a^2}$

b) $\frac{4x^{2-m}\cdot y^{3m}}{7z^{m-n}}÷\frac{5z^{m+n}\cdot x^{3-m}}{14y^{1-2m}}$

c) $\frac{12\frac{1}{x^2}{y}^3}{8z^2}\cdot \frac{4\frac{1}{y^2}z}{3\frac{1}{x^5}}÷\frac{6\frac{1}{z^3}}{2\frac{1}{y^4}z}$

d) $\frac{3^5\cdot 5^7\cdot 11^2\cdot 2^3}{3^4\cdot 5^8\cdot 22^2}$

e) $8^3+2^9+16^2+3\cdot 2^8$

Präfixe, Zehnerpotenzen

Symbol	Name	Ursprung	Wert
T	Tera	(103)4 = 1012	Billion
G	Giga	(103)3 = 109	Milliarde
M	Mega	(103)2 = 106	Million
k	Kilo	(103)1 = 103	Tausend
h	Hekto	102	Hundert
da	Deka	101	Zehn
	Einheit	100	Eins
d	Dezi	10−1	Zehntel
c	Zenti	10−2	Hundertstel
m	Milli	(10−3)1 = 10−3	Tausendstel
μ	Mikro	(10−3)2 = 10−6	Millionstel
n	Nano	(10−3)3 = 10−9	Milliardstel
p	Piko	(10−3)4 = 10−12	Billionstel

Beispiel: 

56 g Eisen (1 Mol) sind 6,022 1023 Teilchen.
  100 g Eisen natürlich 100/56 x 6,022 x 1023 Teilchen
 
100 g Eisen enthalten also: 
100/56 x 6,022 x 1023 Teilchen = 1,075 x 1024 Fe-Atome

Übung:
 
Dichte eines dünnen Hohlzylinders mit recht fiktiven Werten: 
 
Innenradius        $r_i=32mm$
Dicke der Wandung  $d=48\mu m$
Länge              $l=3km$

Masse pro LE       $\mu =234\frac{pg}{nm}$


$\rho =\frac{m}{V}$

$V=\pi \cdot l\cdot (r_a^2-r_i^2)$

Binomische Formeln

Es gelten folgende Formeln:

$(a\pm b{)}^2=a^2\pm 2\cdot a\cdot b+b^2$

$(a+b)\cdot (a-b)=a^2-b^2$

Diese Formeln bieten auch Hilfe beim Kopfrechnen.

Beispielsweise ist

$37^2=(30+7{)}^2=30^2+2\cdot 30\cdot 7+7^2=1369$

Bei Kenntnis der Quadratzahlen bis 20 lassen sich auch viele Multiplikationen auf die dritte binomische Formel zurückführen. Beispielsweise ist

$17\cdot 13=(15+2)\cdot (15-2)=15^2-2^2=225-4=221$

Binomische Formeln lassen sich auch für höhere Potenzen angeben, diese Verallgemeinerung ist der binomische Lehrsatz.später mehr

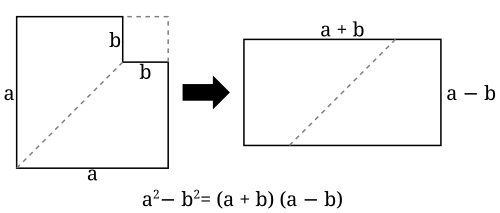
	Nebenstehendes mehrfarbiges Quadrat hat die Seitenlänge (a+b). Wie sofort ersichtlich ist, passen zwei kleinere Quadrate a² und b² hinein, und es bleiben zwei Rechtecke mit der gleichen Fläche a·b übrig. Dadurch ergibt sich $(a+b{)}^2=a^2+b^2+2\cdot a\cdot b$
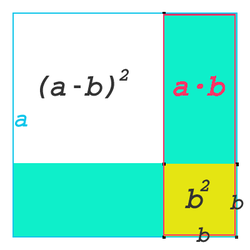
	Im zweiten Bild ist a² das blau umrahmte Quadrat. Soll daraus ein Quadrat der Seitenlänge (a-b) erzeugt werden, wird zuerst die rot umrahmte Fläche a·b abgezogen. Eine ebenso große liegende Fläche kann erst abgezogen werden, wenn zuvor das kleine Quadrat b² addiert wird. Die hier gezeigte Formel lautet also $(a-b{)}^2=a^2-2\cdot a\cdot b+b^2$
	Im dritten Bild ist a² das hell- und dunkelblaue Quadrat. Wird das kleine Quadrat b² davon abgezogen und das verbleibende helle Rechteck gedreht unten angehängt, so entsteht ein Rechteck der Breite (a-b) und der Höhe (a+b). Also ergibt sich die Formel $a^2-b^2=(a+b)\cdot (a-b)$

Eine weitere Veranschaulichung der dritten Binomischen Formel erhält man durch folgende Zerlegung:

quadratische Ergänzung

Die quadratische Ergänzung ist ein Verfahren zum Umformen von Termen, in denen eine Variable quadratisch vorkommt, so dass ein quadriertes Binom entsteht. Es kann zum Beispiel zur Lösung von quadratischen Gleichungen oder zur Bestimmung der Scheitelform (und damit auch des Scheitelpunkts, also des Extremwerts) von quadratischen Funktionen verwendet werden.

Das Verfahren basiert auf dem Zusammenhang

$x^2+ax=\underset{(x+\frac{a}{2}{)}^2}{\underbrace{x^2+ax+\frac{a^2}{4}}}-\frac{a^2}{4}$

Im ersten Schritt wird der Summand ${\left(\frac{a}{2}\right)}^2$ ergänzt, so dass im zweiten Schritt mit Hilfe der 1. Binomischen Formel ein Quadrat gebildet werden kann.

Beispiele:

Gegebene quadratische Funktion:	$y=2x^2-12x+13$
Ausklammern des Leitkoeffizienten:	$y=2(x^2-6x)+13$
Quadratische Ergänzung:	$y=2(x^2-6x+9-9)+13$
Bildung des Quadrats:	$y=2((x-3{)}^2-9)+13$
Ausmultiplizieren:	$y=2(x-3{)}^2-18+13$
Scheitelform der Funktion:	$y=2(x-3{)}^2-5$
Ablesen des Scheitelpunkts:	$S(3|-5)$

 Beispiel:

Gegebene quadratische Gleichung:	$2x^2-12x=32$
Normierung:	$x^2-6x=16$
Quadratische Ergänzung:	$x^2-6x+9=16+9$
Bildung des Quadrats:	$(x-3{)}^2=25$
Wurzelziehen:	$|x-3|=5$
Auflösen der Betragsfunktion:	$x-3=5$ oder $x-3=-5$
Lösungsmenge:	$𝕃=\{-2,8\}$

Übung:

a) ${(3x{y}^2-\frac{4}{5}{x}^3{y}^7)}^2$

b) $(\frac{z^3}{y}+4)(\frac{z^3}{y}-4)$ 

Wandle um!
c) $a^2-b$

d) $\frac{1}{49}{s}^4{t}^2+4s^3{t}^5+196s^2{t}^8$

Vereinfache!
e) $\frac{a^2+2a+1}{a^2-1}$

Quadratische Ergänzug!
f) $3x^2-9x+5$

Wurzeln

Man schreibt die nichtnegative Lösung der Gleichung

$a=x^n$

in der Form

$x=\sqrt[n]{a}$

Man nennt x Wurzel oder Radix, n Wurzelexponent und a Radikand. Erste Umkehrung des Potenzierens. Wobei a und x nichtnegative reelle Zahlen und n>1 eine natürliche Zahl sein sollen. (Schulmathematik) Weicht man davon ab, muß man evtl. Fallunterscheidungen machen bzw. gelten dann nicht mehr alle Potenz- bzw. Wurzelgesetze. Mehr dazu weiter unten.

Vorlage:Achtung

Allgemein gilt daher für geradzahlige Wurzelexponenten 2n:

$\sqrt[2n]{x^{2n}}=|x|$

D.h. der Betrag von x. Einführung Betrag????

Daraus kann man eine wichtige Aussage schlußfolgern:

$a^2=b^2\iff \left|a\right|=\left|b\right|$

Es gilt auch:

$a=b\Rightarrow a^2=b^2$

Aber nicht:

$a^2=b^2\nRightarrow a=b$

Quadrieren ist keine Äquivalenzoperation. Dies wird später beim Lösen von Wurzelgleichungen wieder benötigt.

Die Behandlung von Wurzeln aus negativen Zahlen ist nicht einheitlich. Es gilt beispielsweise

$(-2{)}^3=-8,$

und $-2$ ist die einzige reelle Zahl, deren dritte Potenz $-8$ ist. Allgemein ergeben sich für ungerade Potenzen negativer Zahlen wieder negative Zahlen.

Wurzeln aus negativen Zahlen werden auf zwei Weisen behandelt:

1.Wurzeln aus negativen Zahlen sind generell „verboten“ (Schulmathematik)	2.Es wird zwischen geraden u. ungeraden Wurzelexponenten unterschieden
z.B.ist $\sqrt[3]{-8}$ undefiniert. Die Lösung der Gleichung $x^3=-8$ wird geschrieben als $x=-\sqrt[3]{8}$	Für ungerade Zahlen $2n+1$ gilt generell $\sqrt[2n+1]{-a}=-\sqrt[2n+1]{a}$
$\sqrt[n]{a}$ definiert für a>0	Wurzeln mit geraden Wurzelexponenten aus negativen Zahlen können keine reellen Zahlen sein, weil gerade Potenzen reeller Zahlen nie negativ sind. Dies führte zur Einführung der sogenannten komplexen Zahlen.

Vorlage:Achtung

Das Radizieren mit dem Wurzelexponenten n und das Potenzieren mit dem Exponenten n heben sich gegenseitig auf. Deshalb gilt:

$(\sqrt[n]{a}{)}^n=a$

Das Radizieren mit dem Wurzelexponenten n ist also gleichbedeutend mit dem Potenzieren mit dem Exponenten 1/n. Das zeigt auch die entsprechende Rechenregel:

$(a^{\frac{1}{n}}{)}^n=a^{\frac{n}{n}}=a^1=a$

Also gilt:

$\sqrt[n]{a}=a^{\frac{1}{n}}$

Die Rechenregeln für Wurzeln ergeben sich aus jenen für Potenzen. Für positive Zahlen $a$ und $b$ erhält man leicht folgende Rechengesetze:

$\sqrt[n]{a}\cdot \sqrt[n]{b}=\sqrt[n]{a\cdot b}$

$\sqrt[m]{\sqrt[n]{a}}=\sqrt[m\cdot n]{a}$

$\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}$

${\left(\sqrt[n]{a}\right)}^m=\sqrt[n]{a^m}=a^{\frac{m}{n}}$

$a^{-\frac{m}{n}}=\frac{1}{\sqrt[n]{a^m}}$

Rationalmachen von Nennern

Erweitern, 3.Binom.Formel, Fallunterscheidung

Übung:

a) $\sqrt{0,0121}\sqrt{6,25\cdot 10^6}\sqrt[3]{8,1\cdot 10^{-11}}$

b) $\sqrt{3^2+4^2}\sqrt[3]{3^3+4^3+5^3}$

c) $\sqrt{6}\cdot \sqrt{8}\cdot \sqrt{3}$

d) Teilradizieren:

   $\sqrt{72a^{2}b}\sqrt{131220}\sqrt[3]{9720000}\frac{\sqrt{8}-\sqrt{2}}{\sqrt{8}+\sqrt{2}}$

e) Faktoren in die Wurzel hineinziehen:

   $3\cdot \sqrt{7}4\cdot \sqrt[3]{18}x\cdot \sqrt{1-\frac{y^2}{x^2}}$

f) $\sqrt[3]{0,216}\sqrt[3]{81a^5{b}^7}÷\sqrt[3]{3ab}$

g) ${\left(\sqrt{8}\right)}^{\frac{2}{3}}\cdot {\left(\sqrt{4}\right)}^{\frac{5}{2}}$

h) ${(\sqrt{\frac{a}{b}}+\sqrt{\frac{b}{a}})}^2$

i) $\sqrt{5}\cdot \frac{\sqrt{\frac{3}{10}}+\sqrt{\frac{10}{3}}}{\sqrt{\frac{3}{2}}-\sqrt{\frac{2}{3}}}$

Logarithmen

Die zweite Umkehrung des Potenzierens nennt man Logarithmieren. Für die Lösung der Gleichung

$a=b^x$

schreibt man:

$x={\log }_{b}a$

Aus den Potenzgesetzen lassen sich folgende Rechenregeln ableiten:

${\log }_a(x\cdot y)={\log }_{a}x+{\log }_{a}y$	${\log }_a\frac{x}{y}={\log }_{a}x-{\log }_{a}y$	${\log }_a\left(x^r\right)=r{\log }_{a}x.$
${\log }_a\frac{1}{x}=-{\log }_{a}x$	${\log }_a\sqrt[n]{x}={\log }_a\left(x^{\frac{1}{n}}\right)=\frac{1}{n}{\log }_{a}x.$	$\frac{{\log }_{a}r}{{\log }_{a}b}={\log }_b(r).$

Summen und Differenzen Aus der Formel für Produkte kann eine Formel für Logarithmen von Summen (und Differenzen) wie $x+y$ hergeleitet werden, indem $x$ ausgeklammert wird:

$x+y=x(1+\frac{y}{x}).$

Damit ergeben sich die Regeln

$\begin{array}{cc}{\log }_a(x+y)& ={\log }_{a}x+{\log }_a(1+\frac{y}{x}),\\ {\log }_a(x-y)& ={\log }_{a}x+{\log }_a(1-\frac{y}{x})\end{array}$

Basisumrechnung

Beispiel:
${\log }_{10}8=\frac{{\log }_{2}8}{{\log }_{2}10}\approx \frac{3}{3,32}\approx 0,90.$

Übung:

Ohne Taschenrechner!!
a)${\log }_2\left(\frac{1}{8}\right){\log }_{8}4{\log }_{\sqrt{2}}\left(\frac{1}{2}\right){\log }_{81}\left(\frac{1}{27}\right)$

Umformen!
b)${\log }_a\left(\frac{u^3\cdot \sqrt{u+v}}{a}\right)$

c)${\log }_a\left(\frac{a^7-a^4}{b}\right)$

d)${\log }_2\left(\frac{64u\sqrt{v}}{w}\right)$

e)$\lg \left(\sqrt[3]{2u^2{v}^5}\right)$

Mit Taschenrechner.
f)${\log }_{2}74{\log }_{3}65$

Geometrie I

Strahlensatz

Strahlensatzvarianten

Wenn zwei durch einen Punkt (Scheitel) verlaufende Halbgeraden (Strahlen) von zwei parallelen Geraden geschnitten werden, die nicht durch den Scheitel gehen, dann gelten die folgenden Aussagen:

Es verhalten sich je zwei Abschnitte auf dem einen Strahl, wie die ihm entsprechenden Abschnitte auf dem anderen Strahl.

Beispiel:
AS:BS=CS:DS

Es verhalten sich die ausgeschnittenen Strecken auf den Parallelen, wie die ihnen entsprechenden, vom Scheitel aus gemessenen Strecken auf den Strahlen.

Beispiel:
QP:PM=RT:TM

Es stehen je zwei Abschnitte auf den Parallelen, die einander entsprechen, in gleichem Verhältnis zueinander.

Beispiel:
XZ:YZ=UW:VW

Umkehrung des Strahlensatzes: Ist Eigenschaft 1 erfüllt, so kann man auf parallele Geraden schließen. Ist dagegen Eigenschaft 2 gegeben, so ist ein entsprechender Schluss auf Parallelität nicht möglich.

Datei:ÜbungStrahlensatz1.png

Gleichschenkliges Dreick mit einbeschriebenem Rechteck

Übung:












.

Satzgruppe des Pythagoras

Datei:PythagorasBeweis.png

Satz des Pythagoras

• Satz des Pythagoras

Im rechtwinkligen Dreieck ist die Fläche des Quadrats über der Hypotenuse gleich der Summe der Flächen der Quadrate über den Katheten:

$a^2+b^2=c^2$

• Kathetensatz

Im rechtwinkligen Dreieck ist das Quadrat über einer Kathete flächengleich dem Rechteck aus der Hypotenuse und der Projektion dieser Kathete auf die Hypotenuse:

$a^2=p\cdot c,b^2=q\cdot c$

• Höhensatz

Im rechtwinkligen Dreieck ist das Quadrat über der Höhe auf der Hypotenuse flächengleich mit dem Rechteck aus den Hypotenusenabschnitten.

$h^2=q\cdot p$

Der Satz von Pythagoras liefert eine Formel für den Abstand zweier Punkte in einer Ebene, die durch ein kartesisches Koordinatensystem beschrieben wird. Sind zwei Punkte $(x_0,y_0)$ und $(x_1,y_1)$ gegeben, dann ist ihr Abstand $c$ durch

$c=\sqrt{(x_1-x_0{)}^2+(y_1-y_0{)}^2}$

gegeben. Hierbei wird ausgenutzt, dass die Koordinatenachsen senkrecht zueinander liegen. Dies kann analog auf mehrere Dimensionen erweitert werden und liefert den euklidischen Abstand. Z. B. für den dreidimensionalen Fall:

$c=\sqrt{(x_1-x_0{)}^2+(y_1-y_0{)}^2+(z_1-z_0{)}^2}$

Berechnung von Flächen und Volumina

• Scherung
• Prinzip von Cavallieri